Введение
На прошлой лекции мы изучили, что такое дискретное преобразование Фурье (ДПФ), изучили его свойства, подводные камни, способы улучшения результатов, а также частотно-временное преобразование Фурье.
(1) ![Rendered by QuickLaTeX.com \begin{equation*} X[m] = \sum\limits_{n=0}^{N-1}x[n]\cdot e^{-j2\pi n m/N} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-cf86a4ca3d68483e8a32c8d22b79d019_l3.png)
Из него видно, что для расчёта ![]() -точечного ДПФ требуется
-точечного ДПФ требуется ![]() вычислений с комплексными числами. Получается ресурсозатратно, особенно если мы имеем дело с большим количеством отсчётов.
вычислений с комплексными числами. Получается ресурсозатратно, особенно если мы имеем дело с большим количеством отсчётов.
Учёным не нравилось делать много вычислений, и несколько человек (существуют разные мнения, кто был первым) предложили алгоритмы, позволяющие вычислять ДПФ, производя меньшее количество математических операций. Называются такие алгоритмы Быстрое преобразование Фурье (БПФ).
Хочу сразу отметить, что БПФ возвращает абсолютно такие же результаты, что и ДПФ, использует в основе ту же формулу, только позволяет достичь этих результатов гораздо быстрее.
В рамках данной лекции рассмотрим два самых распространённых алгоритма БПФ — с прореживанием по времени и с прореживанием по частоте.
Итак, выше мы уже отметили, что для ![]() -точечного ДПФ требуется
-точечного ДПФ требуется ![]() операций комплексного умножения и сложения. А что, если разделить исходный сигнал на два длиной
операций комплексного умножения и сложения. А что, если разделить исходный сигнал на два длиной ![]() отсчётов каждый? Тогда получается, что для вычисления ДПФ от одной из половин потребуется
отсчётов каждый? Тогда получается, что для вычисления ДПФ от одной из половин потребуется ![]() математических операций. Или
математических операций. Или ![]() для двух половин (если не считать процедуру разделения и объединения). Получается, эффективность вычислений возрастает в два раза! Но это ещё не предел. Мы можем делить наш сигнал до тех пор, пока не получим набор из сигналов, состоящих из двух отсчётов:
для двух половин (если не считать процедуру разделения и объединения). Получается, эффективность вычислений возрастает в два раза! Но это ещё не предел. Мы можем делить наш сигнал до тех пор, пока не получим набор из сигналов, состоящих из двух отсчётов:
Теперь давайте немного модифицируем выражение (1). Пусть ![]() , тогда:
, тогда:
(2) ![Rendered by QuickLaTeX.com \begin{equation*} X[m] = \sum\limits_{n=0}^{N-1}x[n]\cdot W_N^{n m} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-f36817ebb1fdc959a6dbb522c43e9d99_l3.png)
На примере сигнала из ![]() отсчётов рассчитаем несколько значений
отсчётов рассчитаем несколько значений ![]() :
:
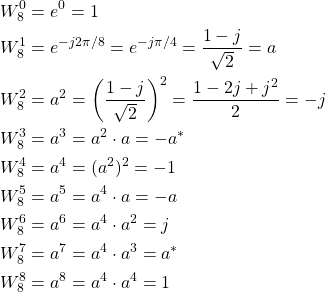
Можно заметить, что первая половина значений ![]() отличается от второй половины только знаком:
отличается от второй половины только знаком:
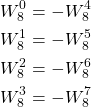
Если произведение ![]() выходит за диапазон от 0 до 7, мы также увидим повторяемость этих значений. Например, при
выходит за диапазон от 0 до 7, мы также увидим повторяемость этих значений. Например, при ![]() , а
, а ![]() :
:
![]()
Следовательно, в процессе ДПФ вычисление одних и тех же значений повторяется несколько раз. Наша задача — оптимизировать процесс так, чтобы избежать выполнение повторяющихся операций.
Алгоритм БПФ с прореживанием по времени
Давайте разделим сигнал на отсчёты с чётными и нечётными номерами, как показано на рисунке:
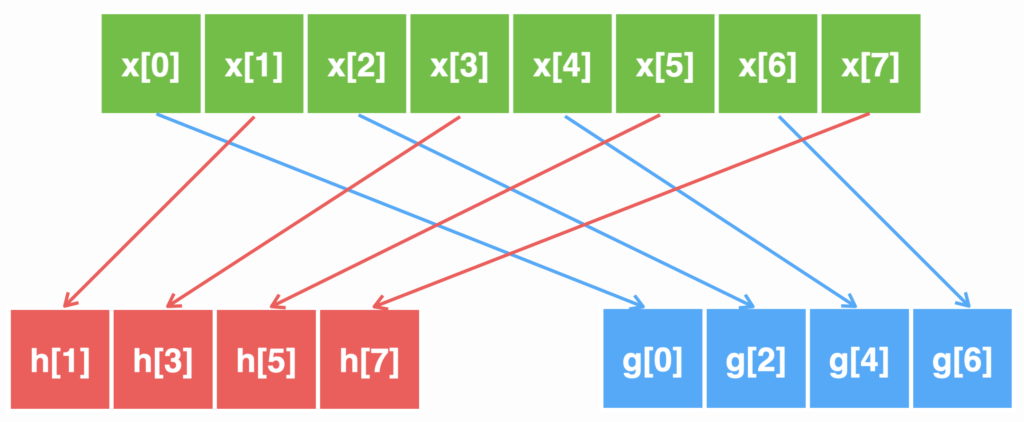
Эта операция называется прореживание по времени. Математически это можно записать следующим образом:
(3) ![Rendered by QuickLaTeX.com \begin{equation*} X[m] = \sum\limits_{n=0}^{N/2-1}x[2n]\cdot W_N^{2nm} + \sum\limits_{n=0}^{N/2-1}x[2n+1]\cdot W_N^{(2n+1)m} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-86a3c21bf0d4f9f39c6f6e9d5fd0bb42_l3.png)
(4) ![]()
(5) ![]()
Тогда, выражение (3) принимает вид:
(6) ![Rendered by QuickLaTeX.com \begin{equation*} X[m] = \sum\limits_{n=0}^{N/2-1}x[2n]\cdot W_{\frac{N}{2}}^{nm} + W_N^m\sum\limits_{n=0}^{N/2-1}x[2n+1]\cdot W_{\frac{N}{2}}^{nm} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-c1cf7a74620aae41070f6baa5690722a_l3.png)
Это был расчёт ДПФ для первых ![]() отсчётов. Теперь запишем подобное выражение для второй половины отсчётов:
отсчётов. Теперь запишем подобное выражение для второй половины отсчётов:
(7) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} X\left[m+\frac{N}{2}\right] = \sum\limits_{n=0}^{N/2-1}x[2n]\cdot W_N^{2n(m+\frac{N}{2})} +\\ +\sum\limits_{n=0}^{N/2-1}x[2n+1]\cdot W_N^{(2n+1)(m+\frac{N}{2})} \end{aligned} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-42125814dd96e278bb03685113bf3f1c_l3.png)
Давайте теперь по очереди разбираться со всеми множителями:
(8) 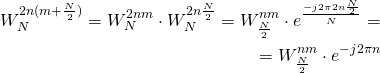
Т.к. ![]() , то выражение (8) принимает вид:
, то выражение (8) принимает вид:
(9) ![]()
Рассмотрим следующий множитель:
(10) ![]()
(11) ![]()
то выражение (10) можно упростить:
(12) ![]()
Подставим результаты из (9) и (12) в уравнение (7) и получим:
(13) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} X\left[m+\frac{N}{2}\right] = \sum\limits_{n=0}^{N/2-1}x[2n]\cdot W_{\frac{N}{2}}^{nm} - \\ - W_N^m\sum\limits_{n=0}^{N/2-1}x[2n+1]\cdot W_{\frac{N}{2}}^{n m} \end{aligned} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-0dfa6676fe3f29ea82df6791f6250282_l3.png)
Для простоты восприятия сделаем две замены:
(14) ![Rendered by QuickLaTeX.com \begin{equation*} G[m] = \sum\limits_{n=0}^{N/2-1}x[2n]\cdot W_{\frac{N}{2}}^{n m} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-e0a2745eec1fe5e42cdec6c032d165e4_l3.png)
(15) ![Rendered by QuickLaTeX.com \begin{equation*} H[m] = \sum\limits_{n=0}^{N/2-1}x[2n+1]\cdot W_{\frac{N}{2}}^{n m} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-f9e8725c2db98da74a8987302852d298_l3.png)
Тогда, с учётом (14) и (15), сгруппируем уравнения (6) и (13):
(16) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} X[m] = G[m]+W_N^m \cdot H[m]\\ X\left[m+\frac{N}{2}\right] = G[m]-W_N^m \cdot H[m] \end{aligned} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-d488decc3632ab54c2380a8d1c10e92d_l3.png)
Полученное выражение (16) называется графом “бабочка”. Почему? Это станет ясно, если посмотреть на его графическое представление:
Данное выражение лежит в основе БПФ с прореживанием по времени.
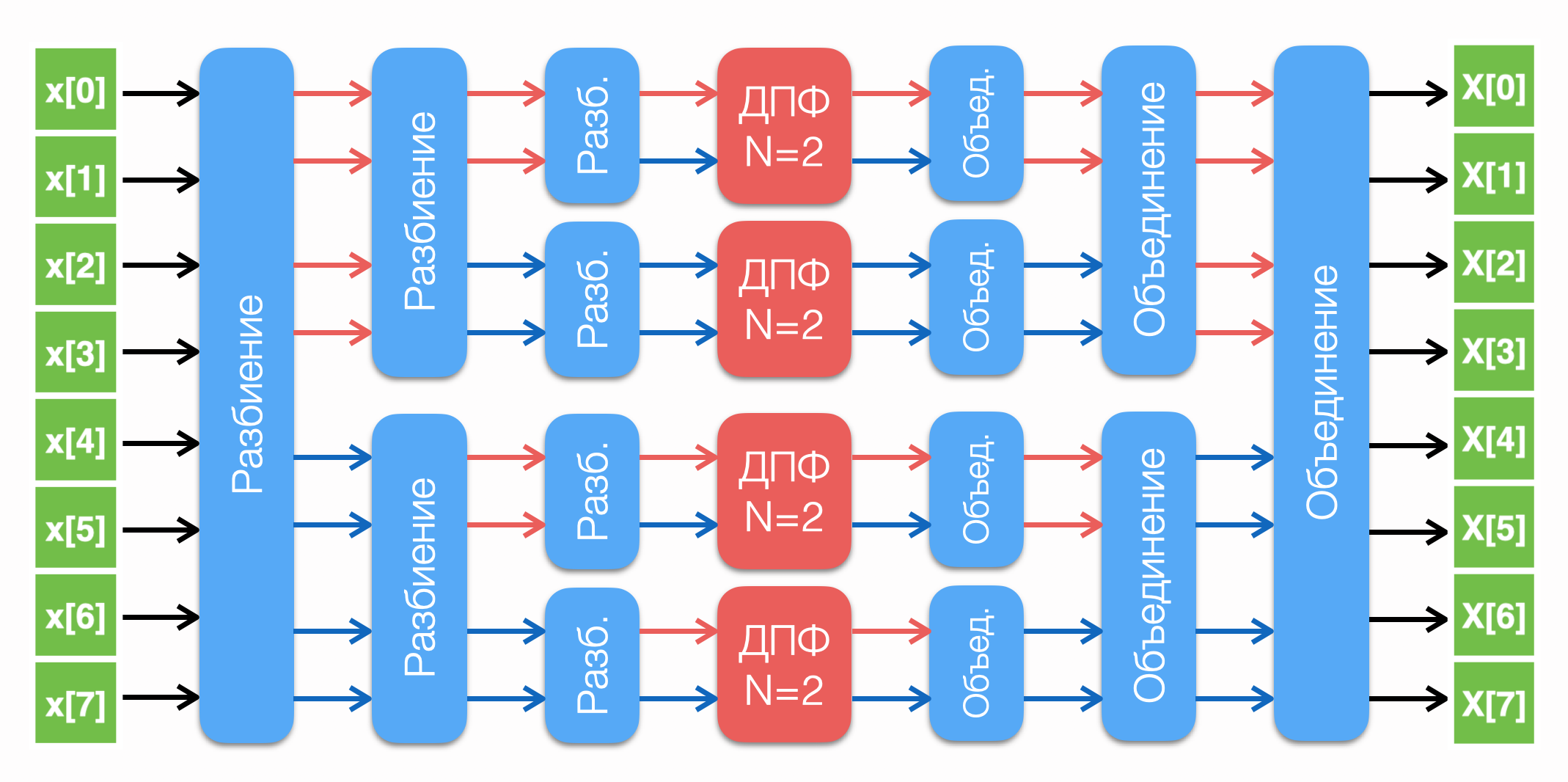
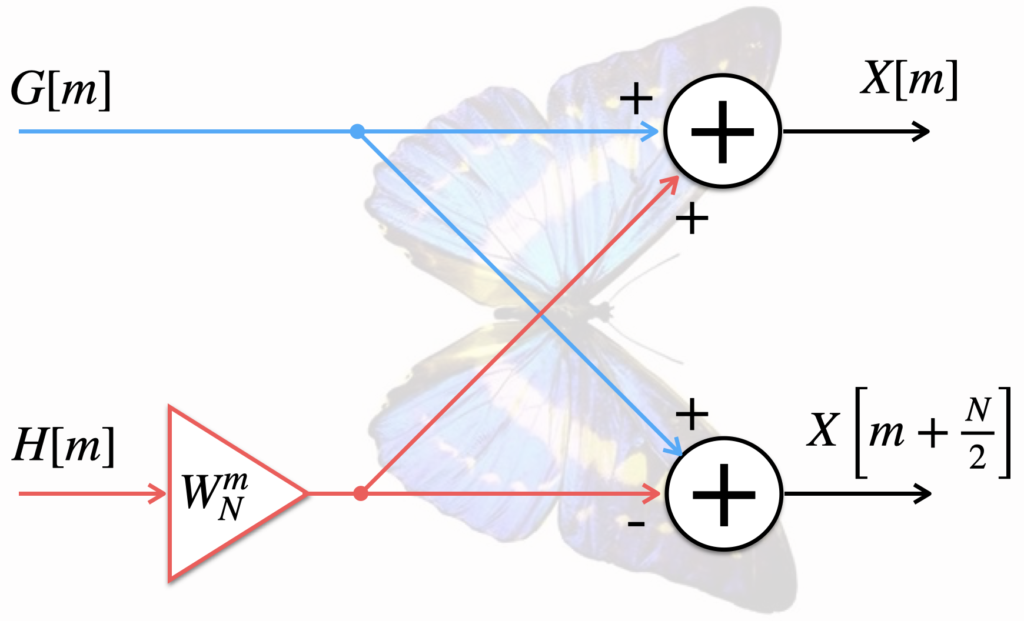
Таким образом, берём анализируемый сигнал и продолжаем разбивать его на сигналы, состоящие из чётных и нечётных индексов до тех пор, пока не получим набор сигналов из двух отсчётов. На рисунке ниже показан пример такого разбиения для сигнала из восьми отсчётов.
Для вычисления ДПФ такого сигнала требуется 3 стадии разбиения. На первом этапе получаем набор из четырёх ДПФ от сигналов из двух отсчётов:
![Rendered by QuickLaTeX.com \begin{align*} X_{00}[0] = x[0] + W_2^0 x[4]\\ X_{00}[1] = x[0] - W_2^0 x[4]\\\\ X_{01}[0] = x[2] + W_2^0 x[6]\\ X_{01}[1] = x[2] - W_2^0 x[6]\\\\ X_{02}[0] = x[1] + W_2^0 x[5]\\ X_{02}[1] = x[1] - W_2^0 x[5]\\\\ X_{03}[0] = x[3] + W_2^0 x[7]\\ X_{03}[1] = x[3] - W_2^0 x[7] \end{align*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-ab877679642b21e33ea0dec0a17505fc_l3.png)
Далее, на основе полученных результатов формируется два ДПФ для сигналов, состоящих из четырёх отсчётов:
![Rendered by QuickLaTeX.com \begin{align*} X_{10}[0] = X_{00}[0] + W_4^0 X_{01}[0]\\ X_{10}[1] = X_{00}[1] + W_4^1 X_{01}[1]\\ X_{10}[2] = X_{00}[0] - W_4^0 X_{01}[0]\\ X_{10}[3] = X_{00}[1] - W_4^1 X_{01}[1]\\\\ X_{11}[0] = X_{02}[0] + W_4^0 X_{03}[0]\\ X_{11}[1] = X_{02}[1] + W_4^1 X_{03}[1]\\ X_{11}[2] = X_{02}[0] - W_4^0 X_{03}[0]\\ X_{11}[3] = X_{02}[1] - W_4^1 X_{03}[1] \end{align*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-2d16b96d70ea0756cb17d591f8796f8d_l3.png)
И на последнем этапе формируются итоговые результаты восьмиточечного ДПФ:
![Rendered by QuickLaTeX.com \begin{align*} X[0] = X_{10}[0] + W_8^0 X_{11}[0]\\ X[1] = X_{10}[1] + W_8^1 X_{11}[1]\\ X[2] = X_{10}[2] + W_8^2 X_{11}[2]\\ X[3] = X_{10}[3] + W_8^3 X_{11}[3]\\ X[4] = X_{10}[0] - W_8^0 X_{11}[0]\\ X[5] = X_{10}[1] - W_8^1 X_{11}[1]\\ X[6] = X_{10}[2] - W_8^2 X_{11}[2]\\ X[7] = X_{10}[3] - W_8^3 X_{11}[3] \end{align*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-c781fe4d25d2de516211f18779d8ae6c_l3.png)
ДПФ рассчитано!
Двоично-инверсная перестановка
Если количество отсчётов исходного сигнала ![]() , где
, где ![]() — целое положительное число, то его разбиение на сигналы, состоящие из чётных и нечётных индексов вплоть до последнего уровня можно сделать легко и за одну итерацию с помощью двоично-инверсной перестановки.
— целое положительное число, то его разбиение на сигналы, состоящие из чётных и нечётных индексов вплоть до последнего уровня можно сделать легко и за одну итерацию с помощью двоично-инверсной перестановки.
Для этого записываем индексы всех отсчётов в двоичной системе счисления, при этом должны быть записаны все ![]() бит индекса, включая ведущие нули. Затем зеркально отображаем код каждого из этих двоичных чисел и записываем полученные результаты обратно в десятичную систему счисления. Готово! Если расставить элементы исходного массива в соответствии с полученными индексами, мы получим подряд идущие пары отсчётов для двухточечного ДПФ. Пример, как это работает для сигнала из восьми отсчётов, представлен в таблице:
бит индекса, включая ведущие нули. Затем зеркально отображаем код каждого из этих двоичных чисел и записываем полученные результаты обратно в десятичную систему счисления. Готово! Если расставить элементы исходного массива в соответствии с полученными индексами, мы получим подряд идущие пары отсчётов для двухточечного ДПФ. Пример, как это работает для сигнала из восьми отсчётов, представлен в таблице:
| Номер до перестановки | Двоичное | Двоично-инверсная перестановка | Десятичное |
|---|---|---|---|
| 0 | 000 | 000 | 0 |
| 1 | 001 | 100 | 4 |
| 2 | 010 | 010 | 2 |
| 3 | 011 | 110 | 6 |
| 4 | 100 | 001 | 1 |
| 5 | 101 | 101 | 5 |
| 6 | 110 | 011 | 3 |
| 7 | 111 | 111 | 7 |
Можете сравнить с рисунком выше, действительно совпадает. Именно поэтому, рассматриваемые нами алгоритмы также называются БПФ по основанию два. У них есть одно небольшое ограничение — количество отсчётов анализируемого сигнала должно быть равно степени двойки (например, 16, 32, 64, 128, 256 и т.д.). “Но как же быть, если, скажем, в моём сигнале всего 200 отсчётов?” — спросите вы. Ничего страшного, нужно просто дополнить сигнал нулевыми отсчётами, пока его длина не станет равна ближайшей степени двойки.
Алгоритм БПФ с прореживанием по частоте
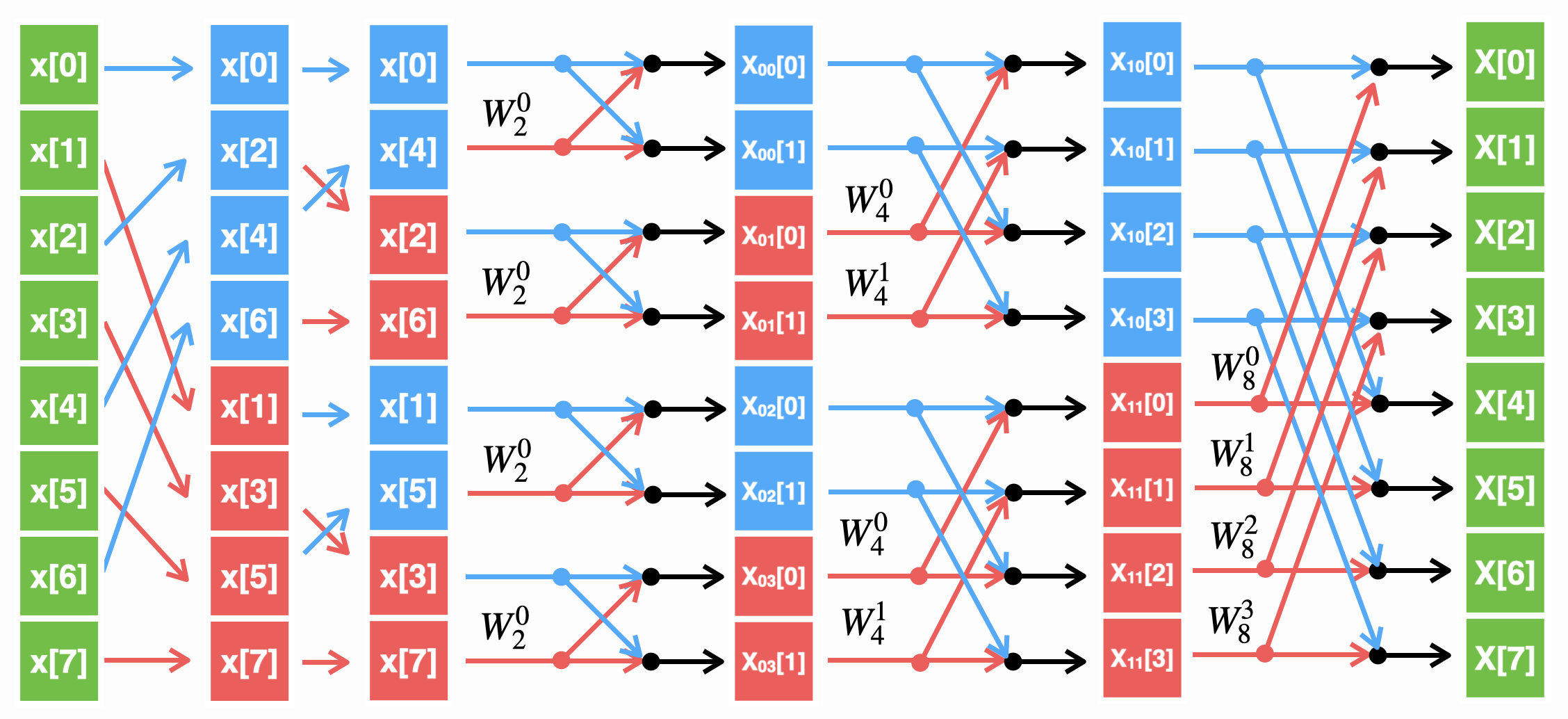
Как вы догадались из названия раздела, прореживать можно не только время, но ещё и частоту. Граф “бабочка” для БПФ с прореживанием по частоте показан на рисунке:
Подробно рассматривать данный алгоритм не будем, просто примем его как данность. Пример БПФ с прореживанием по частоте для сигнала, состоящего из 8 отсчётов показан ниже:
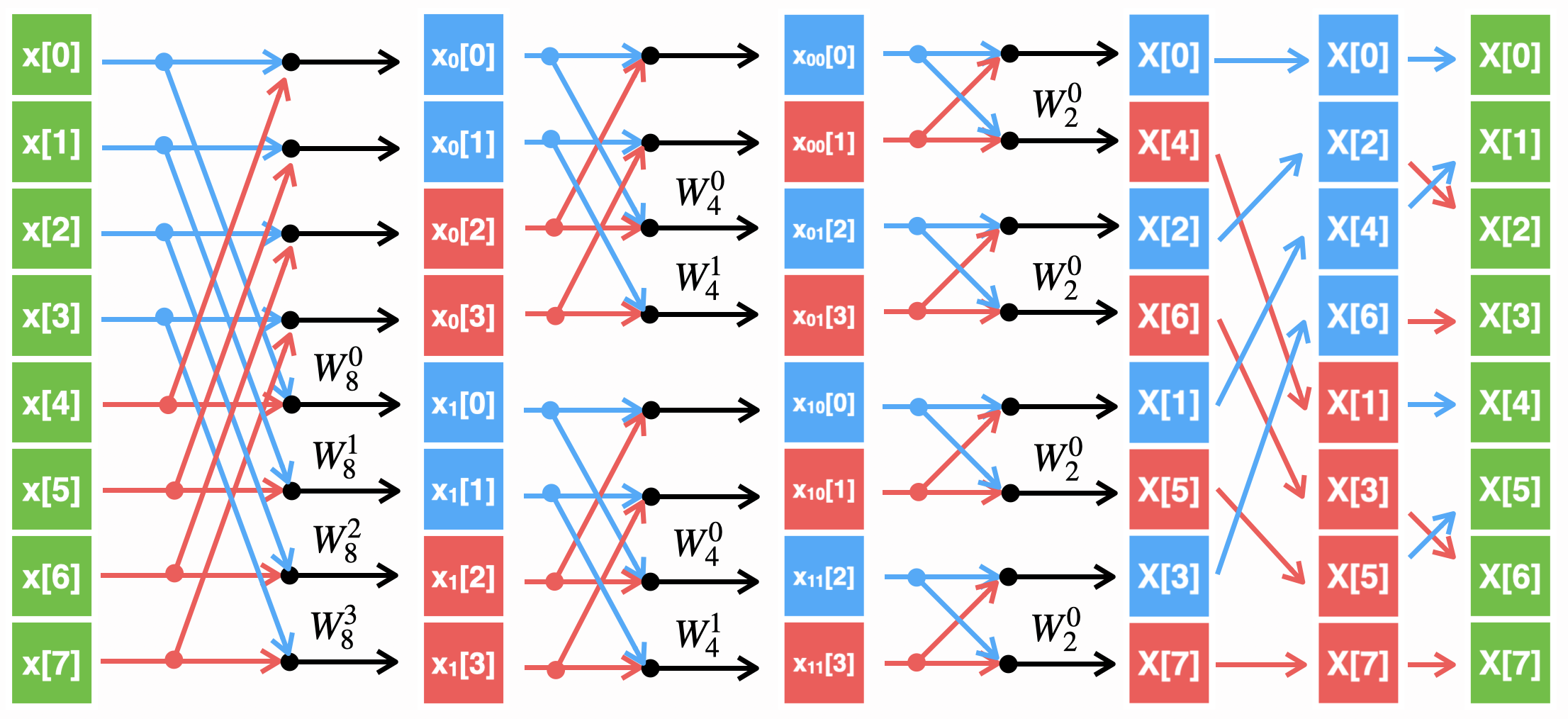
Прореживание (двоично-инверсная перестановка) в данном случае производится уже после вычисления ДПФ, т.е. по частотным отсчётам, отсюда и такое название.
По количеству операций умножения данный алгоритм схож с алгоритмом прореживания по времени, поэтому эффективность их схожая. Какой метод выбрать — решать вам.
Поворотные коэффициенты
В вышеупомянутых “бабочках” есть множитель ![]() . Он называется поворотным коэффициентом. На нижнем уровне БПФ, когда имеем дело с двумя отсчётами, требуется всего один поворотный коэффициент
. Он называется поворотным коэффициентом. На нижнем уровне БПФ, когда имеем дело с двумя отсчётами, требуется всего один поворотный коэффициент ![]() . Умножение на единицу считается тривиальной операцией, откуда следует, что на первом уровне не требуется ни одной операции умножения, только сложение и вычитание.
. Умножение на единицу считается тривиальной операцией, откуда следует, что на первом уровне не требуется ни одной операции умножения, только сложение и вычитание.
На втором уровне у нас получается два поворотных коэффициента ![]() и
и ![]() . Умножение на
. Умножение на ![]() также делается просто: нужно поменять местами действительную и мнимую часть, а также инвертировать знак мнимой части. На этом уровне также не требуется операций умножения.
также делается просто: нужно поменять местами действительную и мнимую часть, а также инвертировать знак мнимой части. На этом уровне также не требуется операций умножения.
На следующем уровне требуется четыре поворотных коэффициента ![]() ,
, ![]() ,
, ![]() и
и ![]() , их значения мы рассчитывали в начале нашей статьи.
, их значения мы рассчитывали в начале нашей статьи.
Давайте проиллюстрируем на графике все упомянутые выше поворотные коэффициенты (и даже немного больше):
Из графика видно, что на каждом следующем уровне количество поворотных коэффициентов увеличивается в два раза, при этом половина из них совпадает с поворотными коэффициентам предыдущего уровня.
Когда БПФ используется для решения каких-либо задач в устройствах цифровой обработки сигналов, количество отсчётов анализируемого сигнала как правило заранее известно и скорее всего не будет меняться в процессе работы устройства. Поэтому, чтобы не тратить время на вычисление ![]() , их заранее рассчитанные значения для заданного количества отсчётов и всех уровней разбиения записывают в памяти в виде таблицы констант, которые в дальнейшем будут использоваться для умножения в графах “бабочка”.
, их заранее рассчитанные значения для заданного количества отсчётов и всех уровней разбиения записывают в памяти в виде таблицы констант, которые в дальнейшем будут использоваться для умножения в графах “бабочка”.
Выводы
БПФ — это всего лишь алгоритм эффективного вычисления ДПФ, поэтому результаты вычисления БПФ и ДПФ получаются абсолютно идентичны.
Для вычисления ДПФ сигнала, состоящего из ![]() отсчётов нам требуется
отсчётов нам требуется ![]() вычислений с комплексными числами, в случае с БПФ —
вычислений с комплексными числами, в случае с БПФ — ![]() вычислений с комплексными числам.
вычислений с комплексными числам.
Чтобы наглядно продемонстрировать эффективность алгоритма, давайте взглянем на таблицу:
| Кол-во отсчётов, N |
Количество вычислений с комплексными числами |
Эффективность | |
|---|---|---|---|
| ДПФ | БПФ | ||
| 256 | 65 536 | 1 024 | 64:1 |
| 512 | 262 144 | 2 304 | 114:1 |
| 1024 | 1 048 576 | 5 120 | 205:1 |
| 2048 | 4 194 304 | 11 264 | 373:1 |
| 4096 | 16 777 216 | 24 576 | 683:1 |
Особенно заметен прирост эффективности с увеличением количества отсчётов.
Скачать конспект в pdf: FFT Lecture – V.V. Leonidov.pdf
Comments (1)