Введение
Цифровой фильтр – фильтр, обрабатывающий цифровой сигнал с целью выделения и (или) подавления определённых частот этого сигнала.
- Разделяют два больших класса цифровых фильтров:
- Фильтры с конечной импульсной характеристикой (КИХ-фильтры, FIR)
- Фильтры с бесконечной импульсной характеристикой (БИХ-фильтры, IIR)
Зачем они нужны? Чем нас не устраивают аналговые фильтры? Давайте рассмотрим преимущества и недостатки цифровых фильтров.
Преимущества цифровых фильтров:
- Высокая точность и воспроизводимость (у аналоговых фильтров это определяется разбросом номиналов компонентов)
- Гибкость (можно изменять характеристику, не затрагивая аппаратную часть)
- Компактность (например, аналоговые ФНЧ могут занимать много места, в то время как цифровые имеют одинаковые габариты при любой форме АЧХ в пределах одной частоты дискретизации)
Недостатки цифвровых фильтров:
- Сложность работы в реальном времени (все вычисления должны пройти менее, чем за один период дискретизации)
- Высокая стоимость
Начнём изучение фильтров с наиболее простого типа — КИХ-фильтров.
КИХ-фильтры
Давайте сразу рассмотрим пример. Сгенерируем в Matlab зашумлённый сигнал частотой 0.5 Гц, оцифрованный с частотй дискретизации 10 Гц. Для начала, объявим переменную fs, которой присвоим значение частоты дискретизации, создадим массив временных отсчётов ts, и переменную N, которой присвоим количество получившихся отсчётов:
fs = 10; ts = 0: 1/fs : 10-1/fs; N = length(ts);
Теперь создадим сам синусоидальный сигнал x с частотой 0.5 Гц, зашумлённый случайным сигналом, амплитуда которого изменяется в диапазоне от a=-0.01 до b=0.1:
a = -0.01; b = 0.1; x = (a + (b - a) * rand(1, N)).*sin(2*pi*0.5*ts);
Построим график сигнала x:
plot(x), grid on;
xlabel('Время');
ylabel('Амплитуда');
title('Сигнал x(n)');
И получим результат:
Возьмём первые пять отсчётов с x(1) по x(5), найдём их среднее арифметическое, запишем его в новый массив в элемент y(1), затем возьмём отсчёты с x(2) по x(6), также рассчитаем их среднее значение и запишем его в элемент y(2) и так далее, пока не пройдём по всему сигналу:
y = zeros(1,N+6); for i = 6 : length(x) y(i) = (x(i-1) + x(i-2) + x(i-3) + x(i-4) + x(i-5))/5; end
А теперь построим сигналы x и y друг под другом в одном окне:
subplot(2,1,1);
plot(x), grid on;
xlabel('Время');
ylabel('Амплитуда');
title('Сигнал x(n)');
subplot(2,1,2);
plot(y(1:100)), grid on;
xlabel('Время');
ylabel('Амплитуда');
title('Сигнал y(n)');
Результаты выполнения получившегося скрипта показаны ниже:
И что же мы видим? Сигнал y(n) (на рисунке снизу) похож на сигнал x(n) (сверху), однако имеет некоторую задержку и более гладкую форму. Получается, что мы только что применили к сигналу x(n) фильтр нижних частот (ФНЧ)! Спроектированный нами фильтр называется скользящее среднее. Уравнение данного фильтра имеет вид:
(1) ![Rendered by QuickLaTeX.com \begin{equation*} y[n]=\sum\limits_{k=0}^{M-1} h(k) \cdot x(n-k) \text{, где} \sum\limits_{k=0}^M h(k) = 1 \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-b1bdff669d80da2fe4508b625186fae0_l3.png)
А его структурная схема выглядит так:
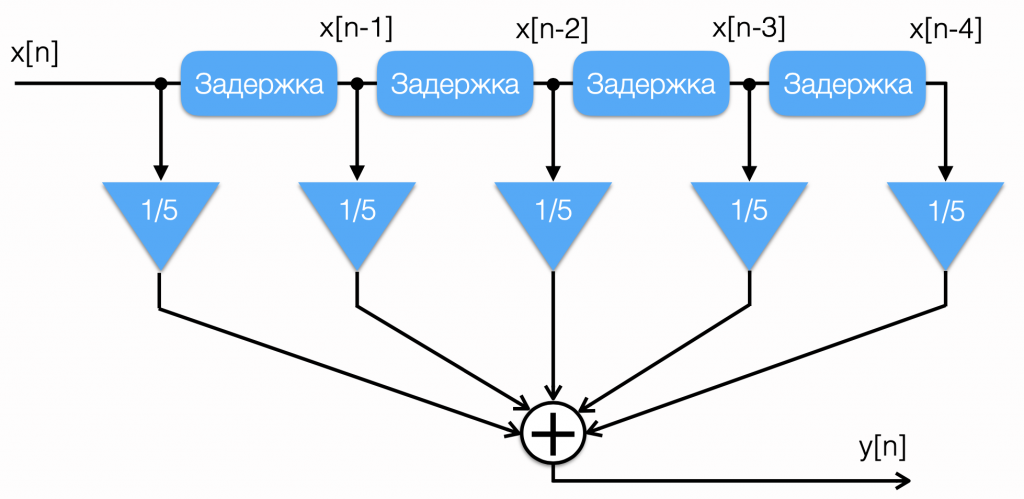
В каждый момент времени берётся текущий отсчёт и 4 предыдущих, каждый из которых домножается на коэффициент 1/5, затем эти результаты складываются и полученная сумма поступает на выход. Процедура повторяется, пока весь сигнал не будет обработан.
Свёртка
А что, если вместо коэффициентов 1/5 взять что-то другое? На самом деле, уравнение (1) представляет собой частный случай операции свёртки:
(2) ![Rendered by QuickLaTeX.com \begin{equation*} y[n] = x[n] \ast h[n]=\sum\limits_{k=0}^{M-1} h(k) \cdot x(n-k), \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-c92c6e0ed841a43340c6de002b1b1e2a_l3.png)
где ![]() ,
, ![]() — длина
— длина ![]() ,
, ![]() — длина
— длина ![]()
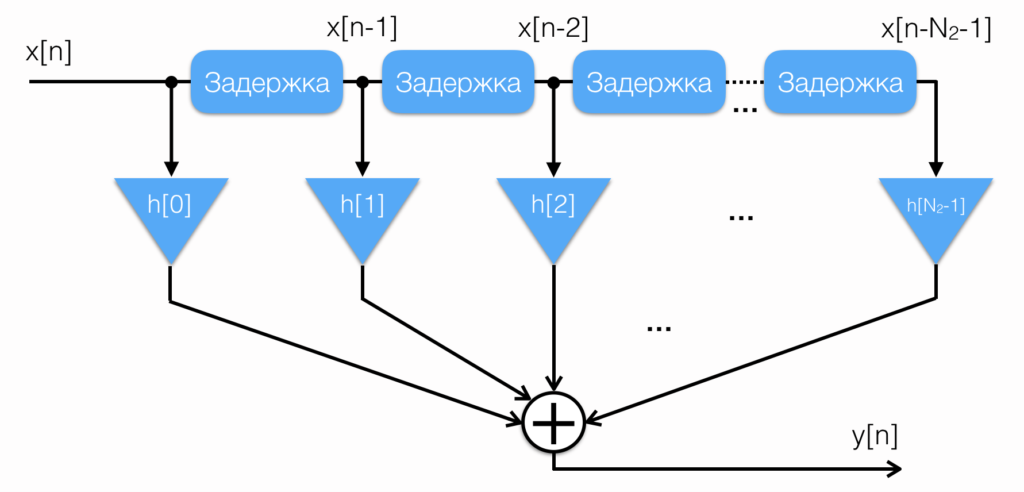
Это уравнение и является уравнением КИХ-фильтра. Его структурная схема выглядит так:
Теорема о свёртке
Со свёрткой связана следующая теорема:
Если два сигнала
и
имеют дискретные преобразования Фурье (ДПФ)
и
соответственно, то свёртка этих сигналов во временной области
эквивалентна произведению их спектров в частотной области
(и наоборот):
(3)
И действует это в обе стороны. Получается, что, когда мы делаем свёртку исходного сигнала с коэффициентами фильтра, мы перемножаем амплитудно-частотную характеристику (АЧХ) исходного сигнала и АЧХ фильтра, тем самым убираем ненужные частоты. А это и есть фильтрация.
Мы выше говорили: “фильтры с конечной импульсной характеристикой, фильтры с бесконечной импульсной характеристикой”. А что же такое “импульсная характеристика”? Давайте вспомним на примере фильтров.
Импульсная характеристика КИХ-фильтра
Импульсная характеристика фильтра — это выходная последовательность фильтра во временной области при подаче на вход фильтра дельта-функции, или функции Дирака — единственного отсчёта, равного единице (единичного импульса), которому предшествуют и за которым следуют нулевые отсчёты.
Возьмём предыдущий пример из Matlab и вместо исходного сигнала x подставим в него функцию Дирака:
clear;
fs = 10;
ts = 0: 1/fs : 10-1/fs;
N = length(ts);
x = zeros(N,1);
x(5) = 1;
subplot(2,1,1);
stem(x), grid on;
xlabel('Время');
ylabel('Амплитуда');
title('Функция Дирака');
y = zeros(1,N+6);
for i = 6 : length(x)
y(i) = (x(i-1) + x(i-2) + x(i-3) + x(i-4) + x(i-5))*1/5;
end
subplot(2,1,2);
stem(y(1:100)), grid on;
xlabel('Время');
ylabel('Амплитуда');
title('Импульсная характеристика');
Результат выполнения скрипта показан ниже:
Из рисунка видно, что импульсная характеристика фильтра представляет собой 5 отсчётов амплитудой 0.2 (или 1/5). Получается, что мы с вами видим ни что иное, как коэффициенты фильтра. Поэтому коэффициенты КИХ-фильтра также называют его импульсной характеристикой.
Проектирование КИХ-фильтров
Теперь возникает вопрос: как рассчитать коэффициенты, чтобы получить требуемую АЧХ фильтра? Самый простой способ: “рисуем” необходимую АЧХ в частотной области, делаем обратное ДПФ от этой АЧХ и получаем набор коэффициентов во временной области. Наверняка, каждый из вас мечтает увидеть фильтр с идеально прямоугольной АЧХ. Возможно ли такое? Давайте разбираться. Что из себя представляет ДПФ от идеально прямоугольного сигнала? Правильно, функцию ![]() , которую мы рассматривали, когда изучали растекание спектра ДПФ:
, которую мы рассматривали, когда изучали растекание спектра ДПФ:
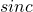
Данная функция бесконечна во временной области, поэтому для реализации идеально прямоугольной АЧХ нам потребуется бесконечное количество коэффициентов фильтра. Получается, чем больше мы используем коэффициентов h[n], тем больше АЧХ фильтра будет похожа на прямоугольную. Вроде бы логично — возьми побольше коэффициентов, получишь хороший фильтр. Но не всё так просто: в реальности мы не можем увеличивать количество коэффициентов фильтра, т.к. это приведёт к дополнительным операциям перемножения, каждая из которых вызывает задержку. Для того, чтобы система работала в реальном времени, нужно, чтобы все вычисления по формуле (2) производились за время, не превышающее один период дискретизации. Вот и простейшее ограничение.
Давайте попробуем на примере. Создадим сигнал x(n), состоящий из N нулевых отсчётов, затем присвоим первым 200 отсчтётам значение 1. Это будет наша требуемая форма АЧХ:
clear; fs = 1000; % частота дискретизации ts = 0:1/fs:1-1/fs; % массив временных отсчётов N = length(ts); % длина массива временных отсчётов x = zeros(N,1); x(1:200) = 1;
Рассчитаем ОДПФ от сигнала x(n), для удобства сдвинем его с помощью ifftshift, отбросим мнимую часть и присвоим полученный результат сигналу y(n). Далее построим графики сигнала x(n), и, чтобы лучше рассмотреть сигнал у(n), график его 200 центральных отсчётов.
y = real(ifftshift(ifft(x)));
subplot(2,1,1);
plot(x), grid on;
xlabel('Частотные отсчёты');
ylabel('Амплитуда');
title('Ожидаемая АЧХ, x(n)');
subplot(2,1,2);
plot(N/2-100:N/2+100-1,y(N/2-100:N/2+100-1)), grid on;
xlabel('Временные отсчёты');
ylabel('Амплитуда');
title('Фрагмент полученной импульсной характеристики, y(n)');
Результат выполнения скрипта показан ниже:
Теперь давайте анализировать реальную АЧХ от спроектированного фильтра. Для этого создадим сигнал a(n), состоящий из N нулевых отсчётов, затем присвоим первому отсчёту 1. Таким образом, получим функцию Дирака, спектр которой является константой на всей частотной оси:
a = zeros(N,1); a(1) = 1;
Теперь попробуем пропустить функцию Дирака через спроектированный ранее фильтр y(n), при этом будем использовать разное количество отсчётов y(n):
figure;
Nf1 = 5;
af1 = filter(y(N/2-Nf1:N/2+Nf1-1),1,a);
subplot(2,2,1);
plot(abs(fft(af1))), grid on;
xlabel('Частотные отсчёты');
ylabel('Амплитуда');
title('АЧХ фильтра, N=10');
Nf2 = 10;
af2 = filter(y(N/2-Nf2:N/2+Nf2-1),1,a);
subplot(2,2,2);
plot(abs(fft(af2))), grid on;
xlabel('Частотные отсчёты');
ylabel('Амплитуда');
title('АЧХ фильтра, N=20');
Nf3 = 25;
af3 = filter(y(N/2-Nf3:N/2+Nf3-1),1,a);
subplot(2,2,3);
plot(abs(fft(af3))), grid on;
xlabel('Частотные отсчёты');
ylabel('Амплитуда');
title('АЧХ фильтра, N=50');
Nf4 = 50;
af4 = filter(y(N/2-Nf4:N/2+Nf4-1),1,a);
subplot(2,2,4);
plot(abs(fft(af4))), grid on;
xlabel('Частотные отсчёты');
ylabel('Амплитуда');
title('АЧХ фильтра, N=100');
Результат выполнения скрипта показан ниже:
Из графиков видно, что, чем больше мы используем отсчётов нашего фильтра (а количество отсчётов – это порядок цифрового фильтра), тем более его характеристика становится похожа на идеальную. Однако, стоит обратить внимание, что на вершине АЧХ всех наших фильтров видны пульсации независимо от того, сколько используется отсчётов в импульсной характеристике. Эти пульсации называются пульсации Гиббса и возникают из-за медленной сходимости ряда Фурье, которая обусловлена наличием разрыва функции на частоте среза полосы пропускания фильтра. С увеличением числа отсчетов уменьшается длительность выбросов на вершине АЧХ, но их амплитуда не меняется и составляет примерно 9% от амплитуды АЧХ на частоте среза.
Окна при проектировании КИХ-фильтров
Запишем выражение (3) следующим образом:
(4) ![]()
где:
![Rendered by QuickLaTeX.com h^\infty[k]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-9a33ee0e13c03d36baef33552e0f6ebb_l3.png) — бесконечная импульсная характеристика идеального фильтра
— бесконечная импульсная характеристика идеального фильтра![Rendered by QuickLaTeX.com w[k]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-ceb0f27caf4b3929a5b12782c0e6911d_l3.png) — окно, наложенное на бесконечную импульсную характеристику
— окно, наложенное на бесконечную импульсную характеристику![Rendered by QuickLaTeX.com H^\infty [m]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-27b4894156b5f4ac60c3ae9fbb1d2957_l3.png) и
и ![Rendered by QuickLaTeX.com W[m]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-fb95909fefd45d8488d8267228b25579_l3.png) — их ДПФ
— их ДПФ
Получается, что, когда мы берём какое-то ограниченное количество отсчётов от импульсной характеристики идеального фильтра, мы умножаем эту импульсную характеристику на прямоугольное окно, спектр которого мы рассматривали выше. Эта процедура во временной области эквивалентна свёртке спектра идеальной характеристики и спектра ограниченной импульсной характеристики в частотной области. Ниже приведён листинг, моделирующий выражение (4):
clear;
fs = 100; % частота дискретизации
ts = -20:1/fs:20-1/fs; % временные отсчёты
N = length(ts); % длина массива временных отсчётов
% Идеальный прямоугольный спектр от бесконечного числа отсчётов
Hinf = zeros(N,1);
Hinf(N/2-750:N/2+749) = 1;
% Спектр прямоугольного окна - sinc(x)
W = sinc(ts);
subplot(2,1,1);
plot(Hinf), grid on, hold on;
plot(W);
xlabel('Частотные отсчёты');
ylabel('Амплитуда');
title('АЧХ фильтра с бесконечной характеристикой Hinf(n) и окна W(n)');
% Свёртка спектров
c = conv(Hinf, W);
subplot(2,1,2);
plot(c), grid on;
xlabel('Частотные отсчёты');
ylabel('Амплитуда');
title('Свёртка Hinf(n) и W(n)');
Результат выполнения скрипта показан ниже:
Чтобы уменьшить амплитуду пульсаций, как и в случае с ДПФ, при проектировании КИХ-фильтров используют окна, отличные от прямоугольного. Давайте модифицируем наш листинг “Анализ АЧХ фильтра, часть 4” и добавим в строчках 26, 34, 42, 50 умножение на окно Хэмминга:
... af1 = filter(y(N/2-Nf1:N/2+Nf1-1).*hamming(Nf1*2),1,a); ... af2 = filter(y(N/2-Nf2:N/2+Nf2-1).*hamming(Nf2*2),1,a); ... af3 = filter(y(N/2-Nf3:N/2+Nf3-1).*hamming(Nf3*2),1,a); ... af4 = filter(y(N/2-Nf4:N/2+Nf4-1).*hamming(Nf4*2),1,a); ...
Полученные результаты показаны ниже:
Другое дело! Пульсации ушли, однако АЧХ фильтра стала более “заваленной”. Выбор типа окна зависит от конкретной решаемой задачи. Самые распространённые: параметрическое окно Кайзера, Чебышёва, окно Блэкмана, Хэмминга и др.
БИХ-фильтры
Основное отличие в структуре БИХ-фильтра от КИХ-фильтра — наличие обратной связи. Что такое обратная связь? Это когда на вход устройства подаётся сигнал, пропорциональный сигналу на его выходе. Таким образом, значение выходного сигнала БИХ-фильтра зависит не только от текущего и предыдущего значения входного сигнала, но и от предыдущего значения выходного сигнала. Это одновременно и плюс, и минус: наличие обратной связи позволяет значительно сократить количество отсчётов (а значит, и порядок фильтра, а как следствие – количество умножений), однако может привести к неустойчивости его работы, или вообще превратить фильтр в генератор. Из-за того, что при отсутствии входного сигнала на выходе БИХ-фильтра может генерироваться бесконечное количество отсчётов, его и прозвали фильтром с бесконечной импульсной характеристикой.
Давайте на примере сравним, сколько же потребуется коэффициентов КИХ- и БИХ-фильтра для реализации одинаковой АЧХ. Спроектируем с помощью filterDesigner два ФНЧ со следующими параметрами:
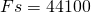 Гц — частота дискретизации;
Гц — частота дискретизации;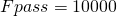 Гц — начало спада АЧХ;
Гц — начало спада АЧХ;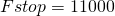 Гц — конец спада АЧХ;
Гц — конец спада АЧХ;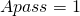 дБ — пульсации в полосе пропускания;
дБ — пульсации в полосе пропускания;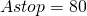 дБ — подавление в полосе задерживания.
дБ — подавление в полосе задерживания.
В результате получили два фильтра, АЧХ и ФЧХ которых представлены ниже:
|
|
|
Из рисунка видно, что АЧХ фильтров действительно схожи, однако, для реализации КИХ-фильтра нам потребовалось 222 коэффициента, а для реализации БИХ-фильтра — всего 41. Получается, что в случае с БИХ-фильтром, операций умножения требуется в 5 раза меньше.
Следует также обратить внимание на график фазы. У КИХ-фильтров ФЧХ гарантированно линейная, у БИХ-фильтров она гарантированно нелинейная, о чём нужно помнить.
Рассмотрим структуру БИХ-фильтра:
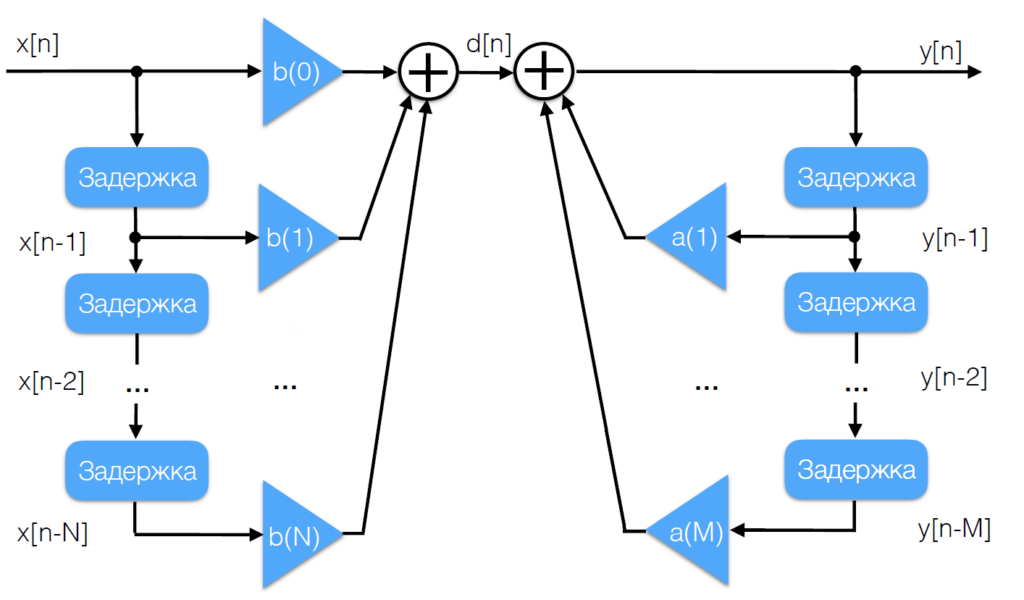
Он состоит из двух частей: прямой и обратной связи. Прямая связь повторяет структурную схему КИХ фильтра, обратная связь напоминает зеркальную копию прямой связи.
Таким образом, разностное уравнение БИХ-фильтра имеет вид:
(5) ![Rendered by QuickLaTeX.com \begin{equation*} y[n] = \sum\limits_{i=0}^{N} b(i) \cdot x(n-i) - \sum\limits_{k=1}^{M} a(k) \cdot y(n-k), \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-8be774d473e364fbb980013abfee0d2b_l3.png)
где:
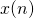 и
и 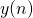 — входной и выходной сигналы соответственно;
— входной и выходной сигналы соответственно;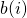 — коэффициенты прямой связи;
— коэффициенты прямой связи;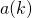 — коэффициенты обратной связи;
— коэффициенты обратной связи;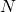 и
и 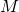 — порядок прямой и обратной связи соответственно;
— порядок прямой и обратной связи соответственно;
При проектировании БИХ-фильтров используют z-преобразование, корни которого идут от преобразования Лапласа. Второе преобразование вам точно знакомо, его должны были изучать на курсе математического анализа. Давайте вспомним, что это такое, а затем перейдём к изучению z-преобразования. Но это на следующей лекции.
Скачать конспект в pdf: Digital Filters Lecture – V.V. Leonidov.pdf
Comments (2)