Введение
Передача информации в современном мире нас окружает повсюду: мобильная связь, интернет, управление воздушным движением и многое другое. Как правило, в качестве “переносчика” информации выступает высокочастотное колебание: 2.4 ГГц и 5 ГГц для Wi-Fi, 2.6 ГГц и другие для 4G, 1030 МГц и 1090 МГц для обмена данными с воздушными судами и т.д. Эти колебания (частоты) называются несущими. Как, используя несущую частоту, закодировать данные? Как передать или получить “0” или “1”? На эти вопросы мы и постараемся ответить.
Процесс изменения одного или нескольких параметров модулируемого несущего сигнала при помощи модулирующего сигнала называется модуляцией.
В рамках данной лекции мы рассмотрим следующие виды модуляции:
- ASK (Amplitude Shift Keying) — амплитудная манипуляция
- BPSK, QPSK (Binary Phase Shift Keying, Quadrature Phase Shift Keying) — фазовая манипуляция
- QASK (Quadrature Amplitude-Shift Keying) — квадратурная манипуляция
- FSK (Frequency Shift Keying), MSK (Minimum Shift Keying) — частотная манипуляция
Амплитудная манипуляция (ASK)
Амплитудная манипуляция — манипуляция, при которой скачкообразно изменяется амплитуда несущего сигнала в зависимости от закодированного сообщения.
Рассмотрим пример. Создадим сигнал fc, который из себя будет представлять несущую частотой 500 Гц, добавим в неё немного шума и промодулируем кодовой последовательностью (сообщением), заданной в массиве code. Логическому “нулю” будет соответствовать амплитуда 0.1, логической “единице” — 1:
clear, clc, close all
fs = 10000;
ts = -0.1 : 1/fs : 0.1-1/fs;
N = length(ts);
%% несущая частота
fc = cos(2*pi*500*ts);
fc = awgn(fc,30);
%% модулирующий сигнал
% длина одного бита в отсчётах
n_for_bit = 200;
% кодируемая последовательность
code = [1 0.1 0.1 1 1 0.1 1 0.1 1 1];
% формируем модулирующий сигнал
fm = zeros(1,N);
for i=1:length(code)
for j=n_for_bit*(i-1)+1:n_for_bit*i
fm(j) = code(i);
end
end
%% амплитудная модуляция
x = fc.*fm;
plot(ts,x,'LineWidth',0.5), grid on, hold on
plot(ts,fm,'LineWidth',2), grid on
title ('ASK модуляция')
xlabel('Время'), ylabel('Амплитуда')
legend({'Модулированный сигнал';'Модулирующий сигнал'})
Результат выполнения скрипта показан ниже:
Из рисунка видно, что амплитуда несущего (модулированного) сигнала — синий график — повторяет форму модулирующего сигнала — оранжевый график.
Теперь давайте сделаем следующую вещь: на комплексной плоскости отметим точки, соответствующие значениям, которые принимает наш закодированный сигнал. В Matlab это можно сделать с помощью функции scatterplot, указав в качестве входных параметров аналитический сигнал (мы его получим с помощью преобразования Гильберта), количество отсчётов на бит (у нас за это отвечает переменная n_for_bit) и смещение от начала сигнала, с которым будут считываться биты (мы хотим считывать биты в их середине, поэтому смещение зададим n_for_bit/2):
%% сигнальное созвездие scatterplot(hilbert(x),n_for_bit,round(n_for_bit/2)), grid on
Посмотрим результат:
Т.к. мнимая часть равна нулю, мы видим два скопления точек вдоль действительной оси: одно вокруг значения 0.1, второе — вокруг 1. Этот график называется сигнальное созвездие. Он часто используется при анализе характеристик модулированных сигналов, т.к. показывает распределение мгновенного значения сигнала на комплексной плоскости в момент его считывания.
Итак, модулированный сигнал есть — попробуем его обратно демодулировать. Наша задача сводится к нахождению огибающей, а как мы выяснили на прошлой лекции — это легко сделать с помощью преобразования Гильберта. Затем создадим что-то вроде цифрового компаратора, с помощью которого зашумлённую огибающую превратим в прямоугольный цифровой сигнал. Дополним наш код:
%% амплитудная демодуляция
% преобразование Гильберта
h = hilbert(x);
figure
subplot(2,1,1)
plot(ts,x,'LineWidth',0.5), grid on, hold on
plot(ts,abs(h),'LineWidth',2), grid on
title ('ASK демодуляция')
xlabel('Время'), ylabel('Амплитуда')
legend({'Модулированный сигнал';'Демодулированный сигнал'})
% компаратор
dem = zeros(1,length(h));
for i=1:length(h)
if abs(h(i))>=0.5
dem(i) = 1;
else
dem(i) = 0;
end
end
subplot(2,1,2)
plot(ts,dem,'LineWidth',2), grid on
title ('Код демодулированного сигнала')
xlabel('Время'), ylabel('Амплитуда')
Смотрим результат:
Как видим, демодулированный сигнал повторяет битовую последовательность, которую мы закодировали изначально в массиве code, а значит мы всё сделали правильно.
Ещё одним типом амплитудной манипуляции является OOK — On-Off Keying. Основное отличие от ASK — логический “ноль” кодируется амплитудой, равной нулю, “единице” соответствует номинальное значение амплитуды сигнала. Если в листинге “ASK-манипуляция, часть 1” в массиве code вместо всех значений 0.1 запишем 0, то как раз получим OOK-манипуляцию.
Фазовая манипуляция (PSK)
Фазовая манипуляция — манипуляция, при которой скачкообразно изменяется фаза несущего сигнала в зависимости от закодированного сообщения.
Начнём с самого простого вида — BPSK — когда у нас всего два значения фазы — ![]() и
и ![]() .
.
Создадим скрипт, реализующий фазовую манипуляцию зашумлённой несущей частоты fc, равной 250 Гц. Кодовую последовательность по аналогии с первым примером будем задавать в массиве code. Перескок фазы будет осуществляться умножением синусоидального сигнала на +1 или -1:
clear, clc, close all
fs = 10000;
ts = 0 : 1/fs : 0.2-1/fs;
N = length(ts);
%% несущая частота
fc = cos(2*pi*250*ts);
fc = awgn(fc,30);
%% модулирующий сигнал
% длина одного бита в отсчётах
n_for_bit = 200;
% кодируемая последовательность
code = [1 -1 -1 1 1 -1 1 -1 1 1];
% формируем модулирующий сигнал
fm = zeros(1,N);
for i=1:length(code)
for j=n_for_bit*(i-1)+1:n_for_bit*i
fm(j) = code(i);
end
end
%% фазовая манипуляция (BPSK)
x = fc.*fm;
plot(ts,x,'LineWidth',0.5), grid on, hold on
plot(ts,fm,'LineWidth',2), grid on
title ('BPSK модуляция')
xlabel('Время'), ylabel('Амплитуда')
legend({'Модулированный сигнал';'Модулирующий сигнал'})
Смотрим, что получилось:
Каждое изменение логического уровня модулирующего сигнала приводит к скачкообразному изменению фазы несущей частоты на ![]() , а это то, что нужно.
, а это то, что нужно.
Теперь дополним код по аналогии с предыдущим примером и построим сигнальное созвездие:
%% сигнальное созвездие scatterplot(hilbert(x),n_for_bit,round(n_for_bit/2)), grid on
Сигнальное созвездие BPSK-сигнала:
Мы имеем два скопления точек: вокруг (-1,0) и (1,0). Эти точки как раз соответствуют повороту вектора единичной длины на ![]() и
и ![]() вокруг начала координат. А значит, модуляция работает корректно.
вокруг начала координат. А значит, модуляция работает корректно.
Теперь наша задача — демодулировать сгенерированный сигнал. Для этого умножим его на несущую частоту fc, а затем применим к полученному сигналу ФНЧ с полосой пропускания 100 Гц, сгенерированный с помощью filterDesigner:
%% BPSK демодуляция
% умножаем сигнал на несущую
y = x.*fc;
% применяем ФНЧ, чтобы убрать несущую
fltr = bpsk_fir;
z = filter(fltr.Numerator,1,y);
figure;
subplot(2,1,1)
plot(ts,y), grid on
title('Модулированный сигнал, умноженный на несущую')
xlabel('Время'), ylabel('Амплитуда')
subplot(2,1,2)
plot(ts,z), grid on
title('Тот же сигнал, прошедший через ФНЧ')
xlabel('Время'), ylabel('Амплитуда')
Получаем результаты:
На верхнем графике наблюдаем синусоиды с частотой 2*fc, имеющие разные постоянные составляющие в зависимости от значения фазы модулированного сигнала. Для того, чтобы получить огибающую, мы воспользовались ФНЧ и получили нижний график. Теперь, чтобы преобразовать данный сигнал в цифровой код, разработаем простейший цифровой компаратор с пороговым значением 0.1 и построим результирующие графики:
% компаратор
dem = zeros(1,length(z));
for i=1:length(z)
if z(i)>=0.1
dem(i) = 1;
else
dem(i) = 0;
end
end
figure
plot(ts,x,'LineWidth',0.5), grid on, hold on
plot(ts,dem,'LineWidth',2), grid on
xlabel('Время'), ylabel('Амплитуда')
title ('BPSK демодуляция')
legend({'Модулированный сигнал';'Демодулированный сигнал'})
Демодулированный сигнал на фоне модулированного сигнала представлен ниже:
Как видим, он повторяет форму модулирующего сигнала, заданного в начале листинга, но имеет временную задержку, возникающую в КИХ-ФНЧ.
В рассмотренном примере модулированный сигнал мог принимать два значения фазы: ![]() и
и ![]() , а значит в один момент времени (такт) можно закодировать только один бит информации — “0” или “1”. Если добавить ещё два изменения фазы (
, а значит в один момент времени (такт) можно закодировать только один бит информации — “0” или “1”. Если добавить ещё два изменения фазы (![]() и
и ![]() ), а затем повернуть полученную диаграмму на
), а затем повернуть полученную диаграмму на ![]() против часовой стрелки, получится QPSK-манипуляция, или квадратурная фазовая манипуляция. В этом случае мы за один такт сможем передавать сразу два бита информации! Посмотрим, как в этом случае будет выглядеть сигнальное созвездие. Разработаем скрипт, который формирует массив случайных данных
против часовой стрелки, получится QPSK-манипуляция, или квадратурная фазовая манипуляция. В этом случае мы за один такт сможем передавать сразу два бита информации! Посмотрим, как в этом случае будет выглядеть сигнальное созвездие. Разработаем скрипт, который формирует массив случайных данных data, которые затем преобразуем в массив значений PSK-сигнала с помощью функции pskmod, в качестве второго параметра которой будет порядок модуляции (для QPSK это M = 4). В качестве третьего параметра данной функции необходимо задать смещение нулевого значения фазы, в нашем случае, как было сказано выше, это ![]() (тогда, в идеальном случае, в каждом квадранте комплексной плоскости будет по одной точке созвездия). Далее добавим немного шума в этот сигнал, чтобы имитировать реальные условия передачи данных и построим сигнальное созвездие:
(тогда, в идеальном случае, в каждом квадранте комплексной плоскости будет по одной точке созвездия). Далее добавим немного шума в этот сигнал, чтобы имитировать реальные условия передачи данных и построим сигнальное созвездие:
clear, clc, close all M = 4; data = randi([0 M-1],1000,1); txSig = pskmod(data, M, pi/M); rxSig = awgn(txSig,20); scatterplot(rxSig), grid on
Получилось вот так:
Мы видим скопление точек вокруг значений ![]() ,
, ![]() ,
, ![]() ,
, ![]() , каждая из которых соответствует положению единичного вектора, начало которого соответствует началу координат, при его повороте с шагом
, каждая из которых соответствует положению единичного вектора, начало которого соответствует началу координат, при его повороте с шагом ![]() . Соответствие фазы и передаваемой информации будет иметь следующий вид:
. Соответствие фазы и передаваемой информации будет иметь следующий вид:
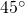 — “11”
— “11”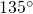 — “01”
— “01”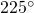 — “00”
— “00”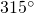 — “10”
— “10”
Это значит, что при при той же самой символьной скорости сигнал с QPSK передаёт в 2 раза больше информации, чем сигнал с BPSK.
Если присвоить M = 8 и убрать из строки 5 параметр pi/M, получим 8-PSK-манипуляцию. Сигнальное созвездие примет вид:
Здесь мы можем передавать за один такт сразу 3 бита. Однако, с увеличением порядка модуляции M, точки созвездия располагаются всё ближе и ближе друг другу, что может привести к ошибкам декодирования такого сигнала, если он сильно зашумлён. Можете поиграться со значениями M и параметром snr функции awgn, чтобы убедиться в этом на примере.
Квадратурная манипуляция (QASK)
QASK (частный случай QAM — Quadrature Amplitude Modulation) — это вид манипуляции, при которой скачкообразно изменяется как амплитуда, так и фаза несущего сигнала, что позволяет за один такт (отсчёт) передать ещё больше информации, чем в рассмотренных ранее видах манипуляции. Можно сказать, что QASK — это комбинация ASK и PSK.
По традиции, сразу начнём с примера. Создадим несущую с частотой 1кГц, помимо этого создадим массив данных data, который будет содержать случайные числа. Зададим порядок модуляции M=16, это значит, что за один такт будем передавать число от 0 до 15, или 4 бита. Один элемент — один такт передачи, количество элементов — 50. Затем создадим массив отсчётов QASK на базе этих данных с помощью функции qammod и построим сигнальное созвездие из полученного набора данных.
clear, clc, close all fs = 10000; ts = 0 : 1/fs : 0.2-1/fs; N = length(ts); %% несущая частота fc = 1000; %% Модуляция M = 16; % порядок QASK модуляции Nd = 50; % размер данных bit_size = N/Nd; % количество отсчётов на бит data = randi([0 M-1],Nd,1); % случайные данные % формируем массив комплексных чисел qdata = qammod(data, M); % сигнальное созвездие sc = scatterplot(qdata); grid on obj = findobj(sc.Children(1).Children, 'type', 'line'); set(obj, 'MarkerSize', 20)
Результат показан ниже:
Это созвездие состоит из 16 групп точек, а значит сформированный сигнал принимает все возможные значения для QASK-манипуляции 16 порядка.
Теперь “поместим” эти данные на несущую частоту. Растянем массив данных до того же количества отсчётов, что и в сигнале несущей частоты (каждый бит повторим bit_size раз) и получим массив qmod. Поэлементно умножим действительные части данного массива на косинус с частотой fc, а мнимые — на синус той же частоты. Просуммируем полученные сигналы (i и q соответственно), в результате чего получим модулированный сигнал y, который готов для передачи. Добавим в него шум для имитации электромагнитных помех и построим графики.
qmod = repelem(qdata,bit_size).'; % размножаем массив данных до кол-ва отсчётов несущей
% формируем синусный и косинусный сигналы
i = real(qmod).*cos(2*pi*fc*ts);
q = imag(qmod).*sin(2*pi*fc*ts);
% суммируем i и q, получаем сигнал, готовый к передаче
y = i+q;
% добавляем шум
y = awgn(y,20);
figure
subplot(3,1,1)
plot(real(qmod)), grid on
title('Действительная часть сигнала')
xlabel('Время'), ylabel('Real')
subplot(3,1,2)
plot(imag(qmod)), grid on
title('Мнимая часть сигнала')
xlabel('Время'), ylabel('Imag')
subplot(3,1,3)
plot(y), grid on
title('Модулированный сигнал')
xlabel('Время'), ylabel('Амплитуда')
Действительная и мнимая части сигнала, а также сам сигнал y можно увидеть на рисунке ниже:
Видно, что в процессе передачи данных изменяется как амплитуда, так и фаза несущей.
Теперь решим обратную задачу: демодулируем сигнал на нижнем графике. Для этого обратно выделим из него синфазную io и квадратурную qo составляющие умножением на косинус и синус несущей частоты соответственно. Чтобы убрать высокочастотную составляющую, как и в BPSK, применим ФНЧ, в результате чего получим сигналы iof и qof, графики которых затем и построим.
%% Демодуляция
io = 2*y.*cos(2*pi*fc*ts);
qo = 2*y.*sin(2*pi*fc*ts);
% применяем ФНЧ, чтобы убрать несущую и умножаем на 2
fltr = qam_fir;
iof = round(conv(fltr.Numerator,io));
qof = round(conv(fltr.Numerator,qo));
figure
subplot(2,1,1)
plot(iof), grid on
title('Синфазная составляющая демодулированного сигнала после ФНЧ')
subplot(2,1,2)
plot(qof), grid on
title('Квадратурная составляющая демодулированного сигнала после ФНЧ')
А вот и графики:
Следует обратить внимание, что при выделении синфазной и квадратурной составляющей, мы также сделали умножение на два (и получили при этом правильные амплитуды). Давайте разбираться, в чём дело. Как было сказано выше, входной сигнал был умножен на функции ![]() и
и ![]() . При умножении на косинус получаем сигнал:
. При умножении на косинус получаем сигнал:
(1) 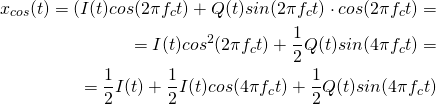
При умножении на синус:
(2) 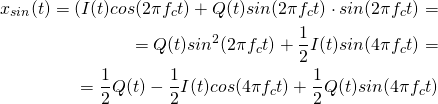
После применения ФНЧ косинусоидальные и синусоидальные составляющие уходят, остаётся только постоянная составляющая:
(3) ![]()
(4) ![]()
Поэтому, чтобы скомпенсировать амплитуду демодулированного сигнала, в строчках 49 и 50 мы и сделали умножение на 2.
Далее преобразуем iof и qof в один комплексный сигнал of, который проредим, взяв из него отсчёты, расположенные в серединах временных отрезков, соответствующих битам данных. Затем воспользуемся функцией qamdemod и сравним результаты: что закодировали, и что в последствии декодировали.
%% Сравнение результатов
% формируем комплесный сигнал после фильтра
of = complex(iof,qof);
% считываем из массива значения с шагом,
% равным периоду следования данных
% и с учётом задержки КИХ-фильтров
fir_delay = round(length(fltr.Numerator)/2);
of_dec = of(fir_delay+round(bit_size/2) : bit_size : length(of)-fir_delay);
% Сравниваем результаты
y = qamdemod(of_dec, M);
figure
plot(data,'b-'), grid on, hold on
plot(y,'x','LineWidth',2)
title('Сравнение закодированных (переданных) и декодированных (принятых) данных')
xlabel('Номер отсчёта'), ylabel('Значение')
legend({'Переданные данные';'Принятые данные'})
Синий график на рисунке отображает входные данные, на основе которых был сформирован модулированный сигнал, красными крестиками — данные, полученные в результате демодуляции этого сигнала:
Как видим, два графика полностью совпадают, а это говорит о том, что реализованный нами алгоритм работает корректно.
Частотная манипуляция (FSK)
Если во всех предыдущих рассмотренных нами видах манипуляции частота несущей была постоянна, то в случае с FSK это не так. FSK — это манипуляция, при которой в зависимости от закодированного сообщения скачкообразно изменяется частота несущего сигнала.
Данный вид манипуляции считается самым помехоустойчивым, т.к. помехи чаще всего влияют на амплитуду, а не на несущую частоту. Частота логического “0” и логической “1” вычисляются по формулам:
(5) ![]()
(6) ![]()
где:
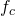 — несущая частота
— несущая частота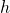 — коэффициент модуляции
— коэффициент модуляции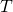 — период передаваемого сообщения
— период передаваемого сообщения
При ![]() манипуляция называется Minimum Shift Keying (MSK) — манипуляция с минимальным сдвигом частоты.
манипуляция называется Minimum Shift Keying (MSK) — манипуляция с минимальным сдвигом частоты.
И снова к примеру. Разработаем скрипт, формирующий FSK-модулированный сигнал. Несущую частоту выберем 500 Гц, индекс модуляции ![]() , период следования битов данных 10 мкс. На основе этого рассчитаем значение двух частот:
, период следования битов данных 10 мкс. На основе этого рассчитаем значение двух частот: f0 и f1, кодирующие логический “0” и “1” соответственно.
clear, clc, close all fs = 10000; ts = 0 : 1/fs : 0.1-1/fs; N = length(ts); %% параметры несущей fc = 500; % несущая частота h = 4; % индекс модуляции T = 10e-3; % длительность бита f0 = fc+h/(2*T); % частота лог. "0" f1 = fc-h/(2*T); % частота лог. "1"
Далее сформируем модулирующий сигнал по аналогии с тем, как мы это делали в примерах с BPSK и ASK:
%% модулирующий сигнал
% длина одного бита в отсчётах
n_for_bit = T*fs;
% кодируемая последовательность
code = [1 0 0 1 1 0 1 0 1 1];
% формируем модулирующий сигнал
fm = zeros(1,N);
for i=1:length(code)
for j=n_for_bit*(i-1)+1:n_for_bit*i
fm(j) = code(i);
end
end
Теперь создадим два сигнала: x0 с частотой f0 и x1 с частотой f1. На базе этих сигналов и модулирующего сигнала fm сформируем модулированный сигнал x и построим графики.
%% Частотная манипуляция
x0 = cos(2*pi*f0*ts);
x1 = cos(2*pi*f1*ts);
x = zeros(1,N);
for i = 1:N
if fm(i) == 0
x(i) = x0(i);
else
x(i) = x1(i);
end
end
plot(ts,x,'LineWidth',0.5), grid on, hold on
plot(ts,fm,'LineWidth',2), grid on
title ('FSK-модуляция')
xlabel('Время'), ylabel('Амплитуда')
legend({'Модулированный сигнал';'Модулирующий сигнал'})
Результат выполнения данного скрипта:
Из рисунка видно, что в зависимости от значения модулирующего сигнала, меняется частота несущей — это то, что нам нужно. Модулировать научились — теперь попробуем это демодулировать. Для этого умножим наш сигнал на косинусоиды с частотами f0 и f1:
%% FSK-демодуляция
% умножаем сигнал на несущую
y0 = x.*x0;
y1 = x.*x1;
figure;
subplot(2,1,1)
plot(ts,y0), grid on
title('Модулированный сигнал, умноженный на f0')
xlabel('Время'), ylabel('Амплитуда')
subplot(2,1,2)
plot(ts,y1), grid on
title('Модулированный сигнал, умноженный на f1')
xlabel('Время'), ylabel('Амплитуда')
Сигналы y0 и y1 показаны ниже:
Теперь найдём разность этих сигналов и пропустим её через ФНЧ:
y = y1 - y0;
% применяем ФНЧ, чтобы оставить постоянную составляющую
fltr = fsk_fir;
z = filter(fltr.Numerator,1,y);
figure
subplot(2,1,1)
plot(ts,y), grid on
title('Сигнал y=y0-y1')
xlabel('Время'), ylabel('Амплитуда')
subplot(2,1,2)
plot(ts,z), grid on
title('Этот же сигнал после ФНЧ')
xlabel('Время'), ylabel('Амплитуда')
Результат показан ниже:
До финала осталось совсем немного — преобразовать нижний график в цифровой сигнал. Для этого, как и в случае с BPSK, воспользуемся цифровым компаратором и построим результирующий график:
% компаратор
dem = zeros(1,length(z));
for i=1:length(z)
if z(i)>=0.1
dem(i) = 1;
else
dem(i) = 0;
end
end
figure
plot(ts,x,'LineWidth',0.5), grid on, hold on
plot(ts,dem,'LineWidth',2), grid on
xlabel('Время'), ylabel('Амплитуда')
title ('FSK-демодуляция')
legend({'Модулированный сигнал';'Демодулированный сигнал'})
Результат демодуляции показан ниже:
Как видим, оранжевый график имеет ту же форму, что и на первоначальном рисунке, но с уже привычной нам временной задержкой, возникающей в цифровом КИХ-фильтре.
Скачать конспект в pdf: Modulation and Demodulation of Digital Signals Lecture – V.V. Leonidov.pdf
Comments (12)