Преобразование Лапласа
Преобразование Лапласа — это интегральное преобразование, связывающее функцию ![]() комплексного переменного (изображения) с функцией
комплексного переменного (изображения) с функцией ![]() вещественного переменного (оригиналом). Используется для решения дифференциальных и интегральных уравнений, а также для анализа динамических систем. Нас сейчас интересует последнее.
вещественного переменного (оригиналом). Используется для решения дифференциальных и интегральных уравнений, а также для анализа динамических систем. Нас сейчас интересует последнее.
Прямое преобразование Лапласа для вещественного ![]() выглядит так:
выглядит так:
(1) 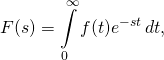
где:
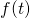 – оригинал;
– оригинал;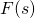 – изображение функции
– изображение функции 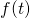 ;
;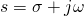 ;
;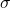 — некое число;
— некое число;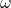 — комплексная частота, рад./с.
— комплексная частота, рад./с.
Т.к. ![]() не имеет размерности,
не имеет размерности, ![]() должен иметь размерность “1/время”, или размерность частоты. Поэтому переменную Лапласа
должен иметь размерность “1/время”, или размерность частоты. Поэтому переменную Лапласа ![]() называют комплексной частотой. А ещё
называют комплексной частотой. А ещё ![]() представляет собой общую форму решения линейных дифуров.
представляет собой общую форму решения линейных дифуров.
По сути, преобразование Лапласа можно рассматривать как непрерывную функцию, значение которой при некотором ![]() представляет собой корреляцию функции
представляет собой корреляцию функции ![]() и затухающей синусоиды
и затухающей синусоиды ![]() , частота которой равна
, частота которой равна ![]() , а коэффициент затухания
, а коэффициент затухания ![]() . Давайте запишем
. Давайте запишем ![]() следующим образом:
следующим образом:
(2) ![]()
![]() — вектор, модуль которого равен единице, вращающийся вокруг начала координат в комплексной плоскости с частотой
— вектор, модуль которого равен единице, вращающийся вокруг начала координат в комплексной плоскости с частотой ![]() . Ещё его называют фазором.
. Ещё его называют фазором. ![]() — комплексное число, равное единице при
— комплексное число, равное единице при ![]() , значение которого увеличивается с увеличением
, значение которого увеличивается с увеличением ![]() . Таким образом,
. Таким образом, ![]() на комплексной плоскости представляет собой спираль:
на комплексной плоскости представляет собой спираль:
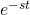 при
при 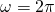 ,
, 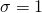
Ниже показана действительная часть ![]() при разных значениях
при разных значениях ![]() , и
, и ![]() :
:
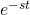 при разных значениях
при разных значениях 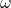 , и
, и 
Получается, что в процессе расчёта ![]() мы делаем корреляцию нашего сигнала с сигналом, имеющим различную сходимость и частоту колебаний. Отсюда можно сделать вывод о поведении анализируемой нами системы. Одной из основных характеристик системы является устойчивость. Простыми словами: система является устойчивой, если при ограниченном входном сигнале, на выходе также получается ограниченный сигнал, который после устранения входного воздействия самостоятельно возвращается к некоторому установившемуся значению.
мы делаем корреляцию нашего сигнала с сигналом, имеющим различную сходимость и частоту колебаний. Отсюда можно сделать вывод о поведении анализируемой нами системы. Одной из основных характеристик системы является устойчивость. Простыми словами: система является устойчивой, если при ограниченном входном сигнале, на выходе также получается ограниченный сигнал, который после устранения входного воздействия самостоятельно возвращается к некоторому установившемуся значению.
Первое, что нам нужно найти при анализе системы — её передаточная характеристика. Это отношение изображения выходного сигнала к изображению входного сигнала при нулевых начальных условиях:
(3) ![]()
Давйте разберём пример. Возьмём передаточную функцию некоторой системы, запишем её изображение в виде:
(4) ![]()
И построим график ![]() :
:
b = [1 2 -1 0];
a = [1 3 2];
omega = linspace(-2.5, 2.5);
sigma = linspace(-2.5, 0.5);
[sigmagrid, omegagrid] = meshgrid(sigma, omega);
sgrid = sigmagrid + 1i*omegagrid;
H = polyval(b, sgrid)./polyval(a, sgrid);
mesh(sigma, omega, abs(H));
xlabel('σ');
ylabel('jω');
zlabel('|H(s)|');
Результат выполнения данного скрипта:
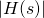
Мы наблюдаем 3D-поверхность, устремляющуюся в бесконечность в двух точках: при ![]() ,
, ![]() и
и ![]() ,
, ![]() . Это полюсы системы. Для того, чтобы найти полюсы системы, нужно прировнять её знаменатель к нулю и найти корни получившегося уравнения. Если проделать аналогичную процедуру с числителем, т.е. найти точки, где
. Это полюсы системы. Для того, чтобы найти полюсы системы, нужно прировнять её знаменатель к нулю и найти корни получившегося уравнения. Если проделать аналогичную процедуру с числителем, т.е. найти точки, где ![]() , мы получим нули системы.
, мы получим нули системы.
Если взять и посмотреть сечение поверхности ![]() при
при ![]() , получим ни что иное, как преобразование Фурье данной системы, или её АЧХ. Это легко проверить, подставив в уравнение (1)
, получим ни что иное, как преобразование Фурье данной системы, или её АЧХ. Это легко проверить, подставив в уравнение (1) ![]() :
:
(5) 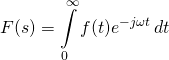
Правда, знакомая формула? Да это и есть преобразование Фурье непрерывного сигнала.
Давайте подробнее рассмотрим полюсы системы. Для этого построим их в двумерной плоскости, где по оси ![]() будет
будет ![]() , по оси
, по оси ![]() –
– ![]() . В Matlab это делается очень просто. Добавим в листинг 1.1 пару строчек:
. В Matlab это делается очень просто. Добавим в листинг 1.1 пару строчек:
Hs = tf(b, a); % передаточная функция iopzmap(Hs), grid on; % график нулей и полюсов
Получим следующий результат:
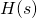
Нули отмечены кружками, полюсы — крестиками.
Если все полюсы системы расположены слева от оси ![]() , система является устойчивой. Если хоть один полюс расположен справа от этой оси — система является неустойчивой. Если все полюсы расположены на оси
, система является устойчивой. Если хоть один полюс расположен справа от этой оси — система является неустойчивой. Если все полюсы расположены на оси ![]() , система находится на границе устойчивости (условно устойчива), к таким системам относят, например, генераторы.
, система находится на границе устойчивости (условно устойчива), к таким системам относят, например, генераторы.
Z-преобразование
Преобразование Лапласа применяют для непрерывных систем, а для анализа интересующих нас дискретных систем используют z-преобразование. Для дискретного сигнала ![]() z-преобразование
z-преобразование ![]() выглядит так:
выглядит так:
(6) ![Rendered by QuickLaTeX.com \begin{equation*} X[z] = \sum\limits_{-\infty}^{+\infty} x[n] \cdot z^{-n}, \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-ab7fecfb328454074ec6f10b88babbc7_l3.png)
где ![]() — комплексное число. Запишем его как
— комплексное число. Запишем его как ![]() , где
, где ![]() — модуль, а
— модуль, а ![]() — аргумент комплексной переменной.
— аргумент комплексной переменной.
Получается, при ![]() выражение (6) принимает вид:
выражение (6) принимает вид:
(7) ![Rendered by QuickLaTeX.com \begin{equation*} X[z]|_{z=e^{j\omega}} = \sum\limits_{-\infty}^{+\infty} x[n] \cdot e^{-j\omega n} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-8dc1e4c1d1c6845512cb3ce3784775a9_l3.png)
Выражение (7) представляет из себя ДПФ от сигнала ![]() . В общем случае,
. В общем случае, ![]() представляет собой поверхность, если взять её сечение цилиндром
представляет собой поверхность, если взять её сечение цилиндром ![]() , то на поверхности данного цилиндра будет отображаться АЧХ нашего дискретного сигнала.
, то на поверхности данного цилиндра будет отображаться АЧХ нашего дискретного сигнала.
Анализ устойчивости здесь производится аналогично анализу с помощью преобразованию Лапласа. За исключением того, что мы смотрим расположение полюсов не относительно оси ![]() , а относительно единичной окружности
, а относительно единичной окружности ![]() , центр которой находится в начале координат. Если все полюсы находятся внутри единичной окружности, система является устойчивой. Если хоть один полюс находится снаружи — система неустойчива. Полюсы, расположенные на единичной окружности говорят об условной устойчивости.
, центр которой находится в начале координат. Если все полюсы находятся внутри единичной окружности, система является устойчивой. Если хоть один полюс находится снаружи — система неустойчива. Полюсы, расположенные на единичной окружности говорят об условной устойчивости.
Рассмотрим пример в пакете Matlab. Возьмём систему с передаточной характеристикой:
(8) ![]()
Это будет прямая связь. И вторую систему:
(9) ![]()
Это будет обратная связь. Далее дискретизируем их с помощью функции c2d (в результате чего получаем ![]() и
и ![]() соответственно) и соединяем согласно схеме, показанной на рисунке ниже (в нашем случае
соответственно) и соединяем согласно схеме, показанной на рисунке ниже (в нашем случае ![]() ):
):
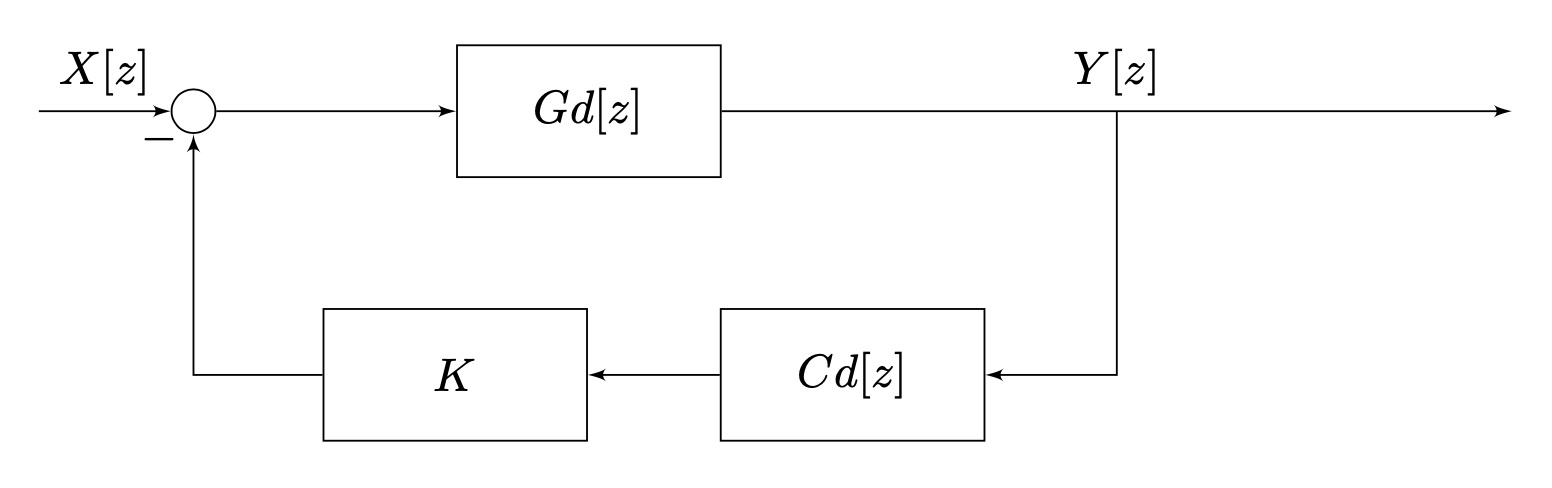
Затем строим график нулей и полюсов получившейся системы на комплексной плоскости:
clear G = tf([0.1 10 5],[1 8 4 2]); Gd = c2d(G,0.1); C = tf([2 1],[2 3]); Cd = c2d(C,0.1); sys = feedback(Gd,Cd); figure rlocus(sys), grid on;
В результате выполнения скрипта получим единичную окружность, на которой крестиками отмечены полюсы системы, кружками – нули системы:
Но, помимо этого, на графике видны кривые разных цветов, которые показывают траекторию движения нулей и полюсов при разном коэффициенте усиления ![]() . Получается, что мы с вами построили корневой годограф. С его помощью можно отследить, при каких значениях
. Получается, что мы с вами построили корневой годограф. С его помощью можно отследить, при каких значениях ![]() система будет устойчивой, а при каких — нет, а также величину пререгулирования при ступенчатом воздействии на сигнал (становится видно, если нажать левой кнопкой мыши на графике). В нашем случае граница устойчивости системы —
система будет устойчивой, а при каких — нет, а также величину пререгулирования при ступенчатом воздействии на сигнал (становится видно, если нажать левой кнопкой мыши на графике). В нашем случае граница устойчивости системы — ![]() . При большем коэффициенте усиления система становится неустойчивой.
. При большем коэффициенте усиления система становится неустойчивой.
Построим графики реакции системы из предыдущего листинга на ступенчатое воздействие (функция Хевисайда, или ступенька — это сигнал, который при ![]() равен нулю, при
равен нулю, при ![]() равен единице). Дополним код:
равен единице). Дополним код:
figure
subplot(2,2,1)
sys1 = feedback(Gd,Cd);
step(sys1), grid on
title('K=1')
subplot(2,2,2)
sys2 = feedback(Gd,Cd*10);
step(sys2), grid on
title('K=10')
subplot(2,2,3)
sys3 = feedback(Gd,Cd*20);
step(sys3), grid on
title('K=20')
subplot(2,2,4)
sys4 = feedback(Gd,Cd*25);
step(sys4), grid on
title('K=25')
Ниже показан результат выполнения данного кода:
Из рисунка видно, что с увеличением ![]() появляются колебания на фронте переходной характеристики. При
появляются колебания на фронте переходной характеристики. При ![]() (больше 21) система не возвращается в состояние равновесия (она неустойчива).
(больше 21) система не возвращается в состояние равновесия (она неустойчива).
Вернёмся к БИХ-фильтрам. Помните, в его структурной схеме были прямоугольники с надписью “Задержка”? Давайте посмотрим, как она выглядит в z-области. Рассмотрим на примере задержки на 1 такт:
(10) ![]()
Запишем z-преобразование для уравнения (10):
(11) ![Rendered by QuickLaTeX.com \begin{equation*} Y[z] = \sum\limits_{-\infty}^{+\infty} x[n-1]z^{-n} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-d0936b53947e9bb6655c43b9b59a6ee6_l3.png)
Пусть ![]() , тогда:
, тогда:
(12) ![Rendered by QuickLaTeX.com \begin{equation*} Y[z] = \sum\limits_{-\infty}^{+\infty} x[k] z^{-(k+1)} = \sum\limits_{-\infty}^{+\infty} x[k] z^{-k}z^{-1} = z^{-1}\sum\limits_{-\infty}^{+\infty} x[k] z^{-k} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-4d28f4ecc3b3ca120006013a7714bf7b_l3.png)
или:
(13) ![]()
Получается, чтобы сделать задержку на 1 такт, достаточно домножить сигнал на ![]() , поэтому во многих структурных схемах фильтров вместо надписи “Задержка” можно увидеть просто
, поэтому во многих структурных схемах фильтров вместо надписи “Задержка” можно увидеть просто ![]() . Задержка на
. Задержка на ![]() тактов выглядит как
тактов выглядит как ![]() .
.
Выражение для БИХ-фильтра в z-области будет выглядеть следующим образом:
(14) ![Rendered by QuickLaTeX.com \begin{equation*} Y[z]=X[z]\sum\limits_{k=0}^{N} b[k] z^{-k}+Y[z]\sum\limits_{k=1}^{M} a[k] z^{-k} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-daf0020760a77d497bdfc448c353564a_l3.png)
Далее, чтобы составить передаточную характеристику, всё, что относится к выходному сигналу, отнесём в числитель, а входного — в знаменатель. Получим:
(15) ![Rendered by QuickLaTeX.com \begin{equation*} H[z] = \frac{Y[z]}{X[z]} = \frac{\sum\limits_{k=0}^{N} b[k] z^{-k}}{1-\sum\limits_{k=1}^{M} a[k] z^{-k}} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-a7dddf189da61c486d7d040d11312de3_l3.png)
Другим не менее важным параметром фильтра является его частотная характеристика. Чтобы её найти, достаточно в его передаточную функцию (15) подставить ![]() :
:
(16) ![Rendered by QuickLaTeX.com \begin{equation*} H[\omega] = H[z]|_{z=e^{j\omega}} = \frac{\sum\limits_{k=0}^{N} b[k] e^{-jk\omega}}{1-\sum\limits_{k=1}^{M} a[k] e^{-jk\omega}} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-fc57cc20640589a9ad1e59c18f343760_l3.png)
Пока это всё.
Скачать конспект в pdf: Laplace and z-transform Lecture – V.V. Leonidov.pdf
Comments (0)