Введение
При спектральном анализе иногда нет необходимости в вычислении полного спектра исследуемого сигнала. Зачастую нас интересует одна или две его частотные составляющие. Реализовывать ради этого полноценный алгоритм быстрого преобразования Фурье (БПФ) — довольно избыточно и затратно по времени (приходится производить большое количество ненужных вычислений). Один из выходов — использовать вместо БПФ обычное дискретное преобразование Фурье (ДПФ) и рассчитывать только частотные составляющие с нужными индексами ![]() :
:
(1) ![Rendered by QuickLaTeX.com \begin{equation*} X[m] = \sum\limits_{n=0}^{N-1} x[n] e^{-j 2 \pi n m / N} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-fad04dbac9548e8ca31905c87a2f0252_l3.png)
Но есть ещё более простой и быстрый путь — это алгоритм Гёрцеля.
Алгоритм Гёрцеля
Данный алгоритм реализуется с помощью БИХ-фильтра-резонатора второго порядка, передаточная характеристика которого имеет вид:
(2) ![]()
Разностное уравнение БИХ-фильтра Гёрцеля выглядит следующим образом:
(3) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} y[n] = u[n]-e^{-j2\pi m/N} u[n-1] \text{, где}\\ u[n] = 2cos(\frac{2\pi m}{N}) \cdot u[n-1] - u[n-2] + x[n] \end{aligned} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-413b4ae0c3846dc3f62383072ce4f8b9_l3.png)
Уравнение (3) можно представить в виде структурной схемы:
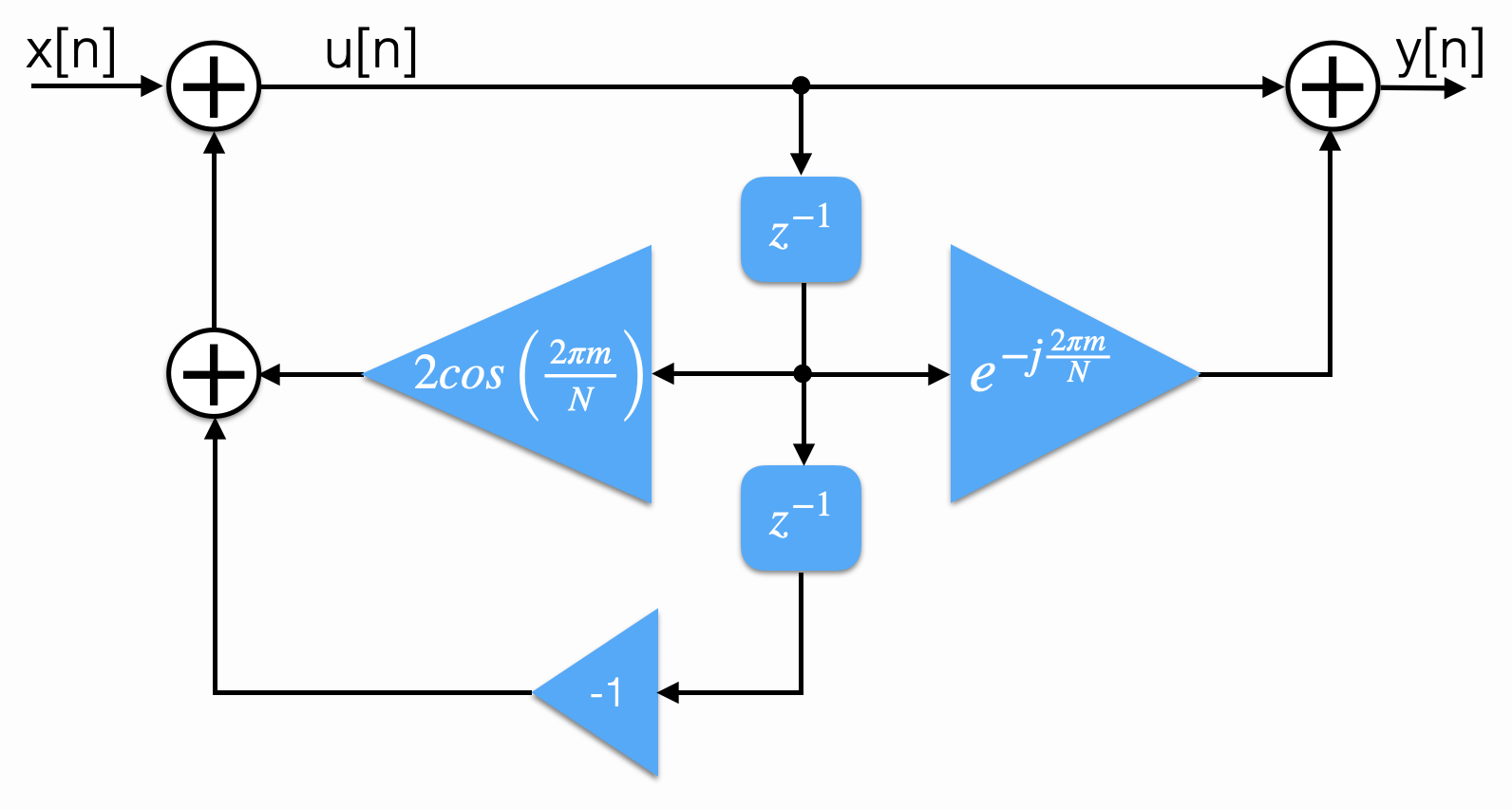
Расчёт значения ![]() из уравнения (3) производится только один раз, после того, как было произведено
из уравнения (3) производится только один раз, после того, как было произведено ![]() расчётов
расчётов ![]() . Итого, для вычисления одной частотной составляющей действительного сигнала с помощью алгоритма Гёрцеля требуется
. Итого, для вычисления одной частотной составляющей действительного сигнала с помощью алгоритма Гёрцеля требуется ![]() операции умножения и
операции умножения и ![]() операций сложения, если не считать расчёт констант
операций сложения, если не считать расчёт констант ![]() и
и ![]() . Для сравнения: в случае расчёта одного бина ДПФ действительного сигнала требуется
. Для сравнения: в случае расчёта одного бина ДПФ действительного сигнала требуется ![]() операций умножения и
операций умножения и ![]() операций сложения, и, вдобавок к этому, необходимо хранить в памяти целую таблицу констант — поворотных коэффициентов. Если считать только затраты на математические операции, алгоритм Гёрцеля почти два раза эффективнее расчёта одного бина ДПФ. Также, нас никто не заставляет брать отсчёты всего сигнала целиком — достаточно взять
операций сложения, и, вдобавок к этому, необходимо хранить в памяти целую таблицу констант — поворотных коэффициентов. Если считать только затраты на математические операции, алгоритм Гёрцеля почти два раза эффективнее расчёта одного бина ДПФ. Также, нас никто не заставляет брать отсчёты всего сигнала целиком — достаточно взять ![]() такое, что в анализируемый сигнал попадёт целое число периодов искомой частоты. И ещё один момент —
такое, что в анализируемый сигнал попадёт целое число периодов искомой частоты. И ещё один момент — ![]() не обязательно должно быть степенью двойки (в отличие от БПФ).
не обязательно должно быть степенью двойки (в отличие от БПФ).
Реализация алгоритма Гёрцеля
Настало время рассмотреть пример. Создадим сигнал, в котором есть две синусоидальные составляющие: одна с частотой 1 кГц амплитудой 1, вторая — с частотой 2 кГц и амплитудой 0.5. Для начала
рассчитаем значение одной из частотных составляющих с индексом m через один бин ДПФ аналогично тому, как делали на лекции по ДПФ, чтобы использовать полученный результат как эталонный:
clear, clc, close all
%% Формируем сигнал из двух гармоник
fs = 8000;
ts = 0 : 1/fs : 0.001-1/fs;
N = length(ts);
x = sin(2*pi*1000*ts) + 0.5*sin(2*pi*2000*ts+3*pi/4);
S = 2*abs(fft(x))/N;
f = 0: fs/N : fs-fs/N;
stem(f,S), grid on, title ('БПФ исходного сигнала')
xlabel('Частота'), ylabel('Амплитуда')
%% Считаем через один отсчёт ДПФ
X = 0;
m = 2;
for n = 1 : N
X = X + x(n)*(cos(2*pi*(n-1)*(m-1)/N)-1i*sin(2*pi*(n-1)*(m-1)/N));
end
X = 2*abs(X)/N; % нормирование амплитуды
% отображение результата
disp(" Расчёт через один бин ДПФ:")
disp(X)
В консоли Matlab увидим что-то вроде:
Расчёт через один бин ДПФ:
0.5000
Всё сходится, по запрашиваемому нами индексу действительно частотная составляющая с амплитудой 0.5 (в этом также можно убедиться по графику БПФ:
А теперь попробуем реализовать алгоритм Гёрцеля. Запишем разностное уравнение (3):
%% Алгоритм Гёрцеля
u1 = 0;
u2 = 0;
w = 2*pi*(m-1)/N;
for n = 1:N
u0 = 2*cos(w)*u1-u2+x(n);
u2 = u1;
u1 = u0;
end
y = u0 - exp(-1i*w)*u2;
Y = 2*abs(y)/N; % нормирование амплитуды
disp(" Расчёт через алгоритм Гёрцеля:")
disp(Y)
И что мы видм в консоли Matlab?
Расчёт через алгоритм Гёрцеля:
0.5000
Тот же самый результат! Можете поменять индекс m и убдеиться, что другие частотные составляющие также определяются правильно.
Давайте модифицируем наш код так, чтобы входным параметром был не индекс частоты, а её значение в Герцах, а заодно попробуем воспользоваться функцией goertzel Matlab и сравним её результаты с нашими:
%% Алгоритм Гёрцеля
fg = 2000; % искомая частота
m = fg/fs*N+1; % вычисление индекса частоты
u1 = 0;
u2 = 0;
w = 2*pi*(m-1)/N;
for n = 1:N
u0 = 2*cos(w)*u1-u2+x(n);
u2 = u1;
u1 = u0;
end
y = u0 - exp(-1i*w)*u2;
Y = 2*abs(y)/N; % нормирование амплитуды
disp(" Амплитуда частотной составляющей fg:")
disp(Y)
H = goertzel(x,m);
H = 2*abs(H)/N;
disp(" Результат выполнения стандартной функции Matlab:")
disp(H)
Получим результат:
Амплитуда частотной составляющей fg:
0.5000
Результат выполнения стандартной функции Matlab:
0.5000
Следует отметить, что переменная ![]() в выражении (3), которая определяет резонансную частоту фильтра Гёрцеля, также может принимать и любые дробные значения в диапазоне от
в выражении (3), которая определяет резонансную частоту фильтра Гёрцеля, также может принимать и любые дробные значения в диапазоне от ![]() до
до ![]() , но на практике этого стараются избегать.
, но на практике этого стараются избегать.
АЧХ фильтра Гёрцеля
Теперь давайте проанализируем АЧХ фильтра Гёрцеля. Для этого через фильтр Гёрцеля с резонансной частотой 2 кГц пропустим синусоидальный сигнал с линейно меняющейся частотой от 1 Гц до частоты Найквиста 4 кГц и посмотрим, что из этого выйдет:
clear, clc, close all
fs = 8000;
ts = 0 : 1/fs : 0.005-1/fs;
N = length(ts);
fg = 2000; % резонансная частота фильтра Гёрцеля
m = fg/fs*N+1; % вычисление индекса резонансной частоты
y = zeros(1,fs/2);
% фильтр Гёрцеля
for k = 1:fs/2
x = sin(2*pi*k*ts);
y(k) = goertzel(x,m);
end
% получение массивов амплитуд и частот
Y = 2*abs(y)/N;
f = 1:fs/2;
% график
plot(f,Y), grid on
title('АЧХ фильтра Гёрцеля с резонансной частотой 2 кГц')
xlabel('Частота'), ylabel('Амплитуда')
А вышло вот что:
Как видно из рисунка, АЧХ фильтра Гёрцеля напоминает всё тот же кардинальный синус ![]() , которым аппроксимируется один бин ДПФ (это мы проходили на одной из прошлых лекций).
, которым аппроксимируется один бин ДПФ (это мы проходили на одной из прошлых лекций).
Выводы
Если требуется проанализировать ![]() частотных составляющих в сигнале из
частотных составляющих в сигнале из ![]() отсчётов, то при
отсчётов, то при ![]() алгоритм Гёрцеля эффективнее, чем БПФ. Помимо этого, алгоритм Гёрцеля требует меньше памяти для хранения констант. Обработка входного сигнала может происходить потоково, с приходом его первого отсчёта, в то время как для расчёта БПФ требуется полный набор отсчётов, количество которых должно быть кратно степени двойки.
алгоритм Гёрцеля эффективнее, чем БПФ. Помимо этого, алгоритм Гёрцеля требует меньше памяти для хранения констант. Обработка входного сигнала может происходить потоково, с приходом его первого отсчёта, в то время как для расчёта БПФ требуется полный набор отсчётов, количество которых должно быть кратно степени двойки.
Скачать конспект в pdf: Goertzel Algorithm Lecture – V.V. Leonidov.pdf
Comments (0)