Аналитический сигнал
В жизни мы обычно имеем дело с действительными сигналами (ток, напряжение, мощность и т.п.), однако, иногда удобно представлять их в виде набора комплексных чисел. Это позволяет точно оценить амплитуду сигнала, его фазу, знак частоты (положительная или отрицательная). Также, для обработки комплексных чисел имеется мощный математический аппарат. Комплексные сигналы широко применяются в цифровой обработке сигналов: получение огибающей, определение мнгновенной частоты, квадратурная модуляция, системы связи, обработка радиолокационных сигналов и другое.
Давайте сразу перейдём к примеру. Создадим сигнал x[n], который представляет из себя косинусоиду частотой 1 кГц, затем создадим второй сигнал, сдвинутый относительно x[n] на ![]() (или синусоиду) и назовём его
(или синусоиду) и назовём его y[n]:
clear, clc, close all
Fs = 40000; % частота дискретизации
ts = 0 : 1/Fs : 0.005-1/Fs; % временные отсчёты
x = cos(2*pi*1000*ts);
y = sin(2*pi*1000*ts);
subplot(2,1,1)
plot(x), grid on, title('x[n]')
xlabel('Время')
ylabel('Амплитуда')
subplot(2,1,2)
plot(x), grid on, hold on, title('x[n] и y[n]')
plot(y), grid on
xlabel('Время')
ylabel('Амплитуда')
Полученные сигналы показаны ниже:
Теперь построим график в трёхмерной системе координат, по оси x будет исходный сигнал x[n] (действительная часть), по оси y сигнал y[n] (мнимая часть), по оси z — время. Также на отдельных графиках покажем проекции полученного сигнала на каждую из плоскостей трёхмерной системы координат:
figure
subplot(2,2,1)
plot3(x,y,ts), grid on, title('Аналитический сигнал')
xlabel('Действительная часть')
ylabel('Мнимая часть')
zlabel('Время')
subplot(2,2,2)
plot(x,y), grid on, title('Проекция x-y')
xlabel('Действительная часть')
ylabel('Мнимая часть')
subplot(2,2,3)
plot(x,ts), grid on, title('Проекция x-z')
xlabel('Действительная часть')
ylabel('Время')
subplot(2,2,4)
plot(y,ts), grid on, title('Проекция y-z')
xlabel('Мнимая часть')
ylabel('Время')
Запускаем скрипт и анализируем полученные результаты:
Рассмотрим первый график: мы видим спираль, вращающуюся вокруг начала координат в плоскости x-y и поднимающуюся “вверх” вдоль оси z. Спираль вращается против часовой стрелки, это значит, что частота сигнала положительная. Правее показана окружность — это проекция данной спирали на плоскость x-y. Радиус данной окружности не изменяется и равен единице, а значит и амплитуда нашего сигнала на протяжении всего времени также не изменяется и равна единице. Ниже показаны проекции спирали на плоскости y-z и x-z: это и есть наши исходные косинусоидальный и синусоидальный сигналы.
Таким образом, любой дискретный сигнал можно представить в виде набора комплексных чисел:
(1) ![]()
где:
![Rendered by QuickLaTeX.com I[n]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-09e3c429b163a8669aff358c85009dcd_l3.png) — In-Phase — синфазная составляющая (действительная часть сигнала)
— In-Phase — синфазная составляющая (действительная часть сигнала)![Rendered by QuickLaTeX.com Q[n]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-7c8d582c51d6124a7336f56126de3f40_l3.png) — Quadrature — квадратурная составляющая (мнимая часть сигнала)
— Quadrature — квадратурная составляющая (мнимая часть сигнала)
Мы уже работали с комплексными числами, когда анализировали результаты ДПФ. Например, для расчёта амплитуды сигнала необходимо найти модуль комплексного числа ![]() :
:
(2) ![]()
А для расчёта фазы сигнала необходимо рассчитать арктангенс:
(3) ![]()
Теперь предположим что,
(4) ![]()
где ![]() — несущая частота сигнала,
— несущая частота сигнала, ![]() — его фаза. Вспомним курс тригонометрии:
— его фаза. Вспомним курс тригонометрии:
(5) ![]()
И преобразуем выражение (4):
(6) ![]()
Т.к. для комплексных чисел справедливо:
(7) ![]()
(8) ![]()
Делаем замену в выражении (6):
(9) ![]()
И получаем ещё одну форму записи аналитического сигнала:
(10) ![]()
Что такое аналитический сигнал — немного разобрались, теперь нужно понять, как его получить из привычного нам действительного сигнала. Эту задачу помогает решить дискретное преобразование Гильберта.
Дискретное преобразование Гильберта
Дискретное преобразование Гильберта представляет собой процедуру, которая на основе исходного сигнала ![]() формирует сигнал
формирует сигнал ![]() , сдвинутый по фазе относительно
, сдвинутый по фазе относительно ![]() на
на ![]() . Иными словами: данное преобразование представляет собой идеальный фазовращатель на
. Иными словами: данное преобразование представляет собой идеальный фазовращатель на ![]() , который называется фильтром Гильберта. Двигать фазу будем с помощью КИХ-фильтра. На предыдущих лекциях мы рассмотрели операцию свёртки, в случае с преобразованием Гильберта её можно записать следующим образом:
, который называется фильтром Гильберта. Двигать фазу будем с помощью КИХ-фильтра. На предыдущих лекциях мы рассмотрели операцию свёртки, в случае с преобразованием Гильберта её можно записать следующим образом:
(11) ![]()
где ![]() — импульсная характеристика фильтра Гильберта, а “
— импульсная характеристика фильтра Гильберта, а “![]() ” обозначает операцию свёртки. Тогда, по теореме о свёртке, ДПФ выходного сигнала преобразования Гильберта есть произведение ДПФ исходного сигнала и ДПФ фильтра Гильберта:
” обозначает операцию свёртки. Тогда, по теореме о свёртке, ДПФ выходного сигнала преобразования Гильберта есть произведение ДПФ исходного сигнала и ДПФ фильтра Гильберта:
(12) ![]()
Исходя из задачи сдвинуть фазу сигнала на ![]() , можно сформулировать следующие требования к фильтру
, можно сформулировать следующие требования к фильтру ![]() :
:
- Все компоненты
![Rendered by QuickLaTeX.com X[\omega]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-5bbc1bb345567cb38daea7c00f015bdc_l3.png) с положительными частотами должны быть сдвинуты на
с положительными частотами должны быть сдвинуты на 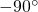
- Все компоненты
![Rendered by QuickLaTeX.com X[\omega]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-5bbc1bb345567cb38daea7c00f015bdc_l3.png) с отрицательными частотами должны быть сдвинуты на
с отрицательными частотами должны быть сдвинуты на 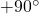
Или, если записать это в виде математического выражения:
(13) ![Rendered by QuickLaTeX.com \begin{equation*} H[\omega]=\begin{cases} j, & \text{при $\omega<0$}.\\ 0, & \text{при $\omega=0$}.\\ -j, & \text{при $\omega>0$}. \end{cases} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-d6c1190b81d5735918cf108901bd74c5_l3.png)
Графическое представление АЧХ и ФЧХ ![]() из выражения (13):
из выражения (13):
Следует обратить внимание, что т.к. ![]() , преобразование Гильберта убирает из сигнала постоянную составляющую.
, преобразование Гильберта убирает из сигнала постоянную составляющую.
Возьмём аналитический сигнал:
(14) ![]()
Спектр данного сигнала с учётом (12) будет иметь вид:
(15) ![]()
Подставим в это выражение ![]() из выражения (13), в результате получим:
из выражения (13), в результате получим:
(16) ![Rendered by QuickLaTeX.com \begin{equation*} S[\omega]=\begin{cases} X[\omega]+j \cdot j \cdot X[\omega], & \text{при $\omega<0$}.\\ X[0], & \text{при $\omega=0$}.\\ X[\omega]-j \cdot j \cdot X[\omega], & \text{при $\omega>0$}. \end{cases} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-137f8121bed370b8a3ddc99400da8295_l3.png)
Упростим выражение (16):
(17) ![Rendered by QuickLaTeX.com \begin{equation*} S[\omega]=\begin{cases} 0, & \text{при $\omega<0$}.\\ X[0], & \text{при $\omega=0$}.\\ 2 \cdot X[\omega], & \text{при $\omega>0$}. \end{cases} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-78f58f132f409cc1efad4d82fc4a5a15_l3.png)
Из (17) можно сделать вывод: спектр аналитического сигнала при отрицательных частотах равен нулю, а при положительных частотах он равен спектру исходного сигнала, умноженному на два. Т.к. постоянная составляющая нас не интересует, ![]() вычислять не будем.
вычислять не будем.
На основе вышесказанного разработаем алгоритм. Чтобы получить аналитический сигнал ![]() , заданный в выражении (14), из действительного сигнала
, заданный в выражении (14), из действительного сигнала ![]() , необходимо выполнить следующую последовательность действий:
, необходимо выполнить следующую последовательность действий:
- Вычислить ДПФ от сигнала
![Rendered by QuickLaTeX.com x[n]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-7678456914fac638e67ac10b23409f76_l3.png) , в результате чего будет получен сигнал
, в результате чего будет получен сигнал ![Rendered by QuickLaTeX.com X[\omega]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-5bbc1bb345567cb38daea7c00f015bdc_l3.png) .
. - Определить индексы отрицательных
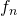 и положительных
и положительных 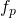 частот
частот ![Rendered by QuickLaTeX.com X[\omega]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-5bbc1bb345567cb38daea7c00f015bdc_l3.png) .
. - Умножить на ноль (или приравнять к нулю) элементы с отрицательными частотами:
![Rendered by QuickLaTeX.com S[f_n] = X[f_n] \cdot 0](https://leonidov.su/wp-content/ql-cache/quicklatex.com-d649d754b8b44ba9f5c5b5ecc79ad9b0_l3.png) .
. - Умножить на 2 элементы с положительными частотами:
![Rendered by QuickLaTeX.com S[f_p] = X[f_p] \cdot 2](https://leonidov.su/wp-content/ql-cache/quicklatex.com-87b83df1f39899ed9006e0fe51c5525d_l3.png) .
. - Вычислить ОДПФ от полученного в п.3 и п.4 сигнала
![Rendered by QuickLaTeX.com S[\omega]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-318b1ea3ae1885fb53cc694c7a296363_l3.png) , в результате будет получен искомый сигнал
, в результате будет получен искомый сигнал ![Rendered by QuickLaTeX.com s[n]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-f1fb78bd4976e34ec3f6e54e4da61b3d_l3.png) .
.
Проверим на практике? Разработаем скрипт, реализующий данный алгоритм (привязка кода к пунктам указана в комментариях):
clear, clc, close all
Fs = 40000;
ts = 0 : 1/Fs : 0.005-1/Fs;
N = length(ts);
% исходный сигнал
x = cos(2*pi*1000*ts);
% вычисление ДПФ, п. 1
X = fft(x);
% поиск индексов положительных и отрицательных частот, п. 2:
fp = 2:floor(N/2)+mod(N,2); % первая половина частот ДПФ - положительные
fn = ceil(N/2)+1+~mod(N,2):N; % вторая половина частот ДПФ - отрицательные
% применение выражения (17), п. 3 и п. 4:
S(fn) = X(fn)*0;
S(fp) = X(fp)*2;
% вычисление ОДПФ, п. 5:
s = ifft(S);
% строим графики:
subplot(2,1,1)
plot(x), grid on, title('Исходный сигнал x[n]')
xlabel('Время')
ylabel('Амплитуда')
subplot(2,1,2)
plot(real(s)), grid on, hold on
plot(imag(s)), grid on, title('Аналитический сигнал s[n]')
xlabel('Время')
ylabel('Амплитуда')
legend({'Действительная часть';'Мнимая часть'})
В результате выполнения скрипта получим графики:
Сверху — исходный сигнал ![]() , снизу — действительная и мнимая часть полученного аналитического сигнала
, снизу — действительная и мнимая часть полученного аналитического сигнала ![]() . Можно сравнить графики, полученные в данном примере, с графиками, полученными в начале лекции. Результаты получились идентичные, из чего можно сделать вывод о корректности работы алгоритма.
. Можно сравнить графики, полученные в данном примере, с графиками, полученными в начале лекции. Результаты получились идентичные, из чего можно сделать вывод о корректности работы алгоритма.
Дискретный фильтр Гильберта
Для того, чтобы можно было использовать фильтр Гильберта как классический цифровой фильтр, нужно рассчитать его импульсную характеристику, а затем подставить её в выражение (11). Расчёт импульсной характеристики цифрового фильтра мы уже проводили на одной из предыдущих лекций: для этого нам нужно взять частотную характеристику фильтра ![]() из выражения (13) и взять от неё ОДПФ.
из выражения (13) и взять от неё ОДПФ.
Запишем выражение ОДПФ для непрерывного сигнала:
(18) 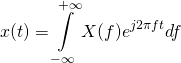
Вместо частоты в Герцах будем использовать круговую частоту: ![]() , тогда
, тогда ![]() . Т.к. частотная характеристика дискретной системы периодична и повторяется с периодом частоты дискретизации
. Т.к. частотная характеристика дискретной системы периодична и повторяется с периодом частоты дискретизации ![]() (или
(или ![]() ), пределы интегрирования установим от
), пределы интегрирования установим от ![]() до
до ![]() :
:
(19) 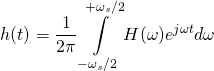
Теперь разобьём интервал интегрирования на две области: ![]() до
до ![]() и от
и от ![]() до
до ![]() :
:
(20) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} h(t) = \frac{1}{2\pi}\int\limits_{-\omega_s/2}^{0} j e^{j \omega t} d\omega + \frac{1}{2\pi}\int\limits_{0}^{+\omega_s/2} -j e^{j \omega t} d\omega = \\ = \frac{j}{2\pi j t}\left[e^{j \omega t}|_{-\omega_s/2}^0 - e^{j \omega t}|_0^{+\omega_s/2}\right] = \\ = \frac{1}{2\pi t}\left[ e^{j0} - e^{-j \omega_s t/2} - e^{j \omega_s t/2} + e^{j0} \right] =\\ = \frac{1}{2\pi t}\left[ 2 - 2\cos(\omega_s t/2) \right] = \frac{1}{\pi t}\left[ 1 - \cos(\omega_s t/2) \right] \end{aligned} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-bbc65dcf7fc533bde20549573c2663db_l3.png)
Следует обратить внимание, что при ![]() получается неопределённость
получается неопределённость ![]() , решить её можно с помощью правила Бернулли—Лопиталя:
, решить её можно с помощью правила Бернулли—Лопиталя:
(21) ![]()
Откуда можно сделать вывод, что ![]() . Для дискретного сигнала результат выражения (20) будет выглядеть следующим образом:
. Для дискретного сигнала результат выражения (20) будет выглядеть следующим образом:
(22) ![]()
(23) ![]()
Построим график импульсной характеристики фильтра Гильберта ![]() для 32 отсчётов и
для 32 отсчётов и ![]() :
:
clear,clc,close all
N = 32;
n = -N/2:N/2-1;
h = 1./(pi*n).*(1-cos(pi*n));
h(N/2+1) = 0;
stem(n,h), grid on, title('Импульсная характеристика фильтра Гильберта')
xlabel('n'), ylabel('h[n]')
xlim([-N/2 N/2-1])
Получим результат:
Теперь проанализируем АЧХ и ФЧХ полученного фильтра:
figure;
% расчёт ДПФ и частотной оси
H = fft(h);
f = (-N/2:N/2-1)*1/N;
% так как мы сдвинули h по оси x из отрицательной области
% на половину его длины вправо,
% применяем теорему о сдвиге ДПФ:
H = H.*exp(-1i*2*pi*f*N/2);
subplot(2,1,1)
plot(f,abs(H),'o-'), grid on
title('АЧХ фильтра Гильберта')
xlabel('\omega/\pi')
ylabel('|H[\omega]|')
phases=[-90;-45;0;45;90];
subplot(2,1,2)
plot(f,angle(H)*180/pi,'o-'), grid on
title('ФЧХ фильтра Гильберта')
xlabel('\omega/\pi')
ylabel('\phi(\omega)')
set(gca, 'YTick', phases)
Получим результат:
Следует обратить внимание, что ![]() — это особенность КИХ-фильтра с антисимметричной импульсной характеристикой. В нашем случае количество отсчётов фильтра чётное, в случае нечётного количества отсчётов мы также будем наблюдать
— это особенность КИХ-фильтра с антисимметричной импульсной характеристикой. В нашем случае количество отсчётов фильтра чётное, в случае нечётного количества отсчётов мы также будем наблюдать ![]() . В связи с этим, на низких частотах АЧХ фильтра заваливается, что будет плохо сказываться на преобразовании низкочастотных составляющих. Также, в области полосы пропускания мы наблюдаем пульсации АЧХ — это эффект Гиббса, который мы изучали на лекции по цифровым фильтрам. Как с этим бороться, мы уже знаем: увеличить порядок фильтра и использовать взвешивание окном. Что мы и сделаем: ниже показаны АЧХ и ФЧХ фильтра Гильберта, взвешенного окном Хэмминга для
. В связи с этим, на низких частотах АЧХ фильтра заваливается, что будет плохо сказываться на преобразовании низкочастотных составляющих. Также, в области полосы пропускания мы наблюдаем пульсации АЧХ — это эффект Гиббса, который мы изучали на лекции по цифровым фильтрам. Как с этим бороться, мы уже знаем: увеличить порядок фильтра и использовать взвешивание окном. Что мы и сделаем: ниже показаны АЧХ и ФЧХ фильтра Гильберта, взвешенного окном Хэмминга для ![]() ,
, ![]() и
и ![]() отсчётов.
отсчётов.
Из графиков видно, что увеличение количества отсчётов и взвешивание импульсной характеристики фильтра Гильберта окном приводит к улучшению АЧХ и ФЧХ фильтра. Теперь полученные коэффициенты можно смело подставлять в выражение (11) и вычислять преобразование Гильберта ![]() через операцию свёртки.
через операцию свёртки.
Однако, есть ещё один момент: сигнал, прошедший через КИХ-фильтр, задерживается на ![]() отсчётов, где
отсчётов, где ![]() — порядок цифрового фильтра. Поэтому, чтобы скомпенсировать линейную фазовую задержку выходного сигнала
— порядок цифрового фильтра. Поэтому, чтобы скомпенсировать линейную фазовую задержку выходного сигнала ![]() относительно входного
относительно входного ![]() , входной сигнал необходимо задержать на
, входной сигнал необходимо задержать на ![]() отсчётов. Рассмотрим пример для фильтра Гильберта 128 порядка:
отсчётов. Рассмотрим пример для фильтра Гильберта 128 порядка:
clear,clc,close all
Nh= 128;
n = -Nh/2:Nh/2-1;
h = 1./(pi*n).*(1-cos(pi*n));
h(Nh/2+1) = 0;
h = h.*hamming(Nh)';
% формируем сигнал с частотой 1кГц
fs = 40000;
ts = 0 : 1/fs : 0.01-1/fs;
N = length(ts);
x = cos(2*pi*1000*ts);
% операция свёртки
y = conv(x,h);
% расчёт необходимой задержки основного сигнала
D = round((Nh-1)/2);
% временной сдвиг основного сигнала
xd = [zeros(1, D), x];
% отображение результатов
subplot(2,1,1)
plot(x), grid on, title('Исходный сигнал')
xlabel('Время')
ylabel('Амплитуда')
xlim([0 500])
subplot(2,1,2)
plot(xd), grid on, hold on
plot(y), title('Применение разработанного фильтра Гильберта к сигналу 1кГц')
xlabel('Время')
ylabel('Амплитуда')
legend({'Действительная часть';'Мнимая часть'})
xlim([0 500])
Результат выполнения скрипта показан ниже:
И графика видно, что сформированная мнимая часть сигнала (оранжевый график снизу) имеет задержку относительно начала координат на 63 отсчёта, на которую также была сдвинута действительная часть сигнала (синий график снизу). В результате получили два синусоидальных сигнала, сдвинутых друг относительно друга на ![]() , которые являются компонентами аналитического сигнала.
, которые являются компонентами аналитического сигнала.
Получение огибающей сигнала
Что такое преобразование Гильберта, разобрались. Но у многих наверняка до сих пор есть вопросы: “Зачем оно нужно? Ну получили сигнал, сдвинутый на ![]() , и что?”. Рассмотрим один из примеров применения: получение огибающей модулированного сигнала.
, и что?”. Рассмотрим один из примеров применения: получение огибающей модулированного сигнала.
Создадим несущий сигнал частотой 1 кГц, который будет модулирован частотой 50 Гц и построим его график:
clear, clc, close all
fs = 40000;
ts = 0 : 1/fs : 0.05-1/fs;
N = length(ts);
% несущая частота
fc = cos(2*pi*1000*ts);
% модулирующий сигнал
fm = sin(2*pi*50*ts);
% модулированный сигнал
x = fc.*fm;
plot(ts,x), grid on, title('Амплитудно-модулированный сигнал')
xlabel('Время'), ylabel('Амплитуда')
График полученного сигнала:
Теперь разработаем ФНЧ со следующими параметрами:
- Fs = 40000 Гц
- Fpass = 500 Гц
- Fstop = 2000 Гц
- Astop = 60 дБ
Затем возьмём модуль модулированного сигнала x и применим к нему вышеуказанный фильтр (функцию фильтра я здесь показывать не буду, она генерируется с помощью пакета filterDesigner):
%% Использование ФНЧ
lp_f = lp_filter;
y = filter(lp_f.Numerator,1,abs(x));
figure
plot(ts,x), grid on, hold on
plot(ts,y), ylim([-1 1])
title('Получение огибающей с помощью ФНЧ')
xlabel('Время'), ylabel('Амплитуда')
legend({'Несущая частота';'Огибающая'})
Получим график:
Из графика видно, что огибающая (оранжевый сигнал) напоминает реальную огибающую нашего сигнала только отдалённо. Если мы будем менять параметры фильтра, мы всё равно не сможем получить идеальный сигнал, повторяющий модуль синусоиды 50 Гц с единичной амплитудой. Попробуем применить полученные сегодня знания и получить огибающую сигнала с помощью преобразования Гильберта:
%% Преобразование Гильберта
z = hilbert(x); % стандартная функция SP Toolbox
figure
plot(ts,x), grid on, hold on
plot(ts,abs(z)), ylim([-1 1])
title('Получение огибающей с помощью преобразования Гильберта')
xlabel('Время'), ylabel('Амплитуда')
legend({'Несущая частота';'Огибающая'})
Результат показан ниже:
Другое дело, правда?
Выводы
Итак, мы рассмотрели два способа расчёта аналитического сигнала:
- Через прямое и обратное ДПФ.
- Через операцию свёртки с использованием импульсной характеристики фильтра Гильберта.
Первый способ даёт меньше искажений, однако требует большего количества математических операций. Второй способ более простой с точки зрения вычислений, однако не обеспечивает полное подавление отрицательных частот и плохо работает в области низких частот.
Также на практике показали, как можно применить преобразование Гильберта для получения огибающей модулированного сигнала.
Скачать конспект в pdf: Hilbert Transform Lecture – V.V. Leonidov.pdf
Comments (4)