Введение
Ранее для анализа нестационарных сигналов мы рассматривали такой инструмент спектрального анализа, как частотно-временное преобразование Фурье. Мы брали окно фиксированной ширины, разбивали исследуемый сигнал на участки, равные ширине данного окна, брали ДПФ от каждого такого участка, а затем строили график в трёхмерной системе координат, показывающий, какие частотные составляющие в какой момент времени присутствуют в исследуемом сигнале. В качестве недостатка такого преобразования мы отметили неопределённость: чем уже окно, тем лучше разрешение по времени и хуже по частоте; чем шире окно — тем лучше разрешение по частоте и хуже по времени. В случае, если в сигнале частоты по времени распределены неравномерно, этот метод не очень подходит, в таких случаях используют Вейвлет-преобразование (Wavelet transform), которое позволяет иметь хорошее разрешение по времени на высоких частотах, а на низких — по частоте.
Давайте в очередной раз вспомним, что из себя представляет преобразование Фурье в тригонометрической форме записи:
(1) ![Rendered by QuickLaTeX.com \begin{equation*} X[m] = \sum\limits_{n=0}^{N-1} x[n] \left({ \cos\frac{2 \pi n m}N - j \sin\frac{2 \pi n m}N }\right) \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-b83227073a3964c2a365ca896501995a_l3.png)
Можно сказать, что это корреляция исследуемого сигнала ![]() с набором синусоид и косинусоид с частотами
с набором синусоид и косинусоид с частотами ![]() , где
, где ![]() — индекс частоты,
— индекс частоты, ![]() — частота дискретизации,
— частота дискретизации, ![]() — количество отсчётов.
— количество отсчётов.
Идея вейвлет-преобразования схожа, только вместо набора синусоид и косинусоид будут использоваться другие функции, которые называются вейвлетами.
Вейвлеты
В переводе с английского вейвлет (wavelet) — это “маленькая волна”, а по факту — это математическая функция (обозначим её ![]() ), которая должна удовлетворять следующим условиям:
), которая должна удовлетворять следующим условиям:
- Среднее значение функции должно быть равно нулю (площадь под графиком, находящимся ниже оси x должна быть равна площади под графиком, находящимся над осью x):
(2)
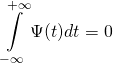
- Функция должна обладать конечной энергией (иными словами, она должна быть локализована на временной оси):
(3)
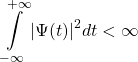
Рассмотрим несколько таких функций. Возьмём косинусоидальный сигнал, который умножим на Гауссову функцию, а затем построим график полученного сигнала и его ДПФ:
clear, clc, close all
fs = 50;
T = 5;
ts = -T:1/fs:T-1/fs;
c = cos(2*pi*ts); %косинусоида
g = exp(-ts.^2/2); %Гауссова функция
w = c.*g; %произведение Гаусса на синусоиду
subplot(4,1,1)
plot(ts, c), grid on
title('Косинусоидальный сигнал')
xlabel('Время'),ylabel('Амплитуда')
subplot(4,1,2)
plot(ts, g), grid on
title('Гауссова функция')
xlabel('Время'),ylabel('Амплитуда')
subplot(4,1,3)
plot(ts, w), grid on
title('Вейвлет Морле')
xlabel('Время'),ylabel('Амплитуда')
%ДПФ вейвлета
W = abs(fft(w));
N = length(w);
f = 0:fs/N:fs-fs/N;
subplot(4,1,4)
plot(f(1:N/2),W(1:N/2)), grid on
title('ДПФ вейвлета Морле')
xlabel('Частота'),ylabel('Амплитуда')
Результат показан ниже:
Полученная функция называется вейвлетом Морле. И она действительно удовлетворяет сформулированным выше условиям. Если посмотреть на график ДПФ, увидим что-то, напоминающее узкополосный фильтр, который позволяет выделить из анализируемого сигнала заданную частоту.
Если взять вторую производную от Гауссовой функции g, получим ещё один вейвлет, который из-за своей причудливой формы называется “Мексиканская шляпа”:
clear, clc, close all
fs = 50;
T = 5;
ts = -T:1/fs:T-1/fs;
g = exp(-ts.^2/2); % Гауссова функция
dg = -diff(g,2); % вторая производная от Гауссовой функции
subplot(2,1,1)
plot(ts(1:length(ts)-2), dg), grid on
title('Вейвлет "Мексиканская шляпа"')
xlabel('Время'),ylabel('Амплитуда')
%ДПФ вейвлета
W = abs(fft(dg));
N = length(dg);
f = 0:fs/N:fs-fs/N;
subplot(2,1,2)
plot(f(1:N/2),W(1:N/2)), grid on
title('ДПФ вейвлета "Мексиканская шляпа"')
xlabel('Частота'),ylabel('Амплитуда')
График вейвлета “Мексиканская шляпа” показан ниже:
Действительно, похоже на шляпу. Спектр данного вейвлета также похож на узкополосный фильтр, но имеет более узкую полосу пропускания, чем у вейвлета Морле.
И ещё один вейвлет, который мы рассмотрим — это дискретный вейвлет Хаара. Он представляется выражением:
(4) ![Rendered by QuickLaTeX.com \begin{equation*} \Psi[x]=\begin{cases} 1, & \text{при $0 \leq x< 1/2$}.\\ -1, & \text{при $1/2 \leq x< 1$}.\\ 0, & \text{при $x \notin [0,1)$}.\end{cases} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-25e7a130344667ebe80e6ae64c6db8b2_l3.png)
Проиллюстрируем выражение (4) с помощью Matlab, а заодно построим ДПФ вейвлета Хаара:
clear, clc, close all
fs = 100;
T = 1.5;
ts = -T:1/fs:T-1/fs;
N = length(ts);
x = zeros(1,N);
x((ts >= 0) & (ts < 0.5)) = 1; x((ts >= 0.5) & (ts < 1)) = -1;
plot(ts, x, 'LineWidth',2), grid on
title('Дискретный вейвлет Хаара')
xlabel('Время'),ylabel('Амплитуда')
Получим следующий результат:
Наверняка вы обратили внимание, что спектр данного вейвлета имеет уже знакомую нам форму функции ![]() , это связано с его прямоугольной формой.
, это связано с его прямоугольной формой.
Существует большое множество вейвлетов, мы рассмотрели самые базовые из них. Теперь давайте разбираться, что с ними делать.
Вейвлет-преобразование
Из каждой рассмотренной выше функции (назовём их материнскими вейвлетами) можно составить целые семейства вейвлетов. Каждый материнский вейвлет можно, во-первых, масштабировать (растянуть или сжать), а во-вторых, сдвинуть влево или вправо вдоль временной оси. Таким образом, вейвлет можно записать в виде следующей функции:
(5) ![]()
где ![]() — масштаб,
— масштаб, ![]() — временной сдвиг.
— временной сдвиг.
Теперь, по аналогии с ДПФ, запишем выражение для вейвлет-преобразования:
(6) 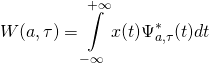
где ![]() — анализируемый сигнал,
— анализируемый сигнал, ![]() — комплексно-сопряженный вейвлет.
— комплексно-сопряженный вейвлет.
Получается, что в процессе вейвлет-преобразования мы находим корреляцию исходного сигнала с набором вейвлетов, каждый из которых имеет различный масштаб и сдвиг относительно начала исследуемого сигнала. В случае, если сигнал на каком-либо участке похож на заданный вейвлет с заданным масштабом, мы увидим всплеск функции ![]() .
.
Чтобы понять разницу между частотно-временным ДПФ и вейвлет-преобразованием, нужно взглянуть на рисунок ниже:
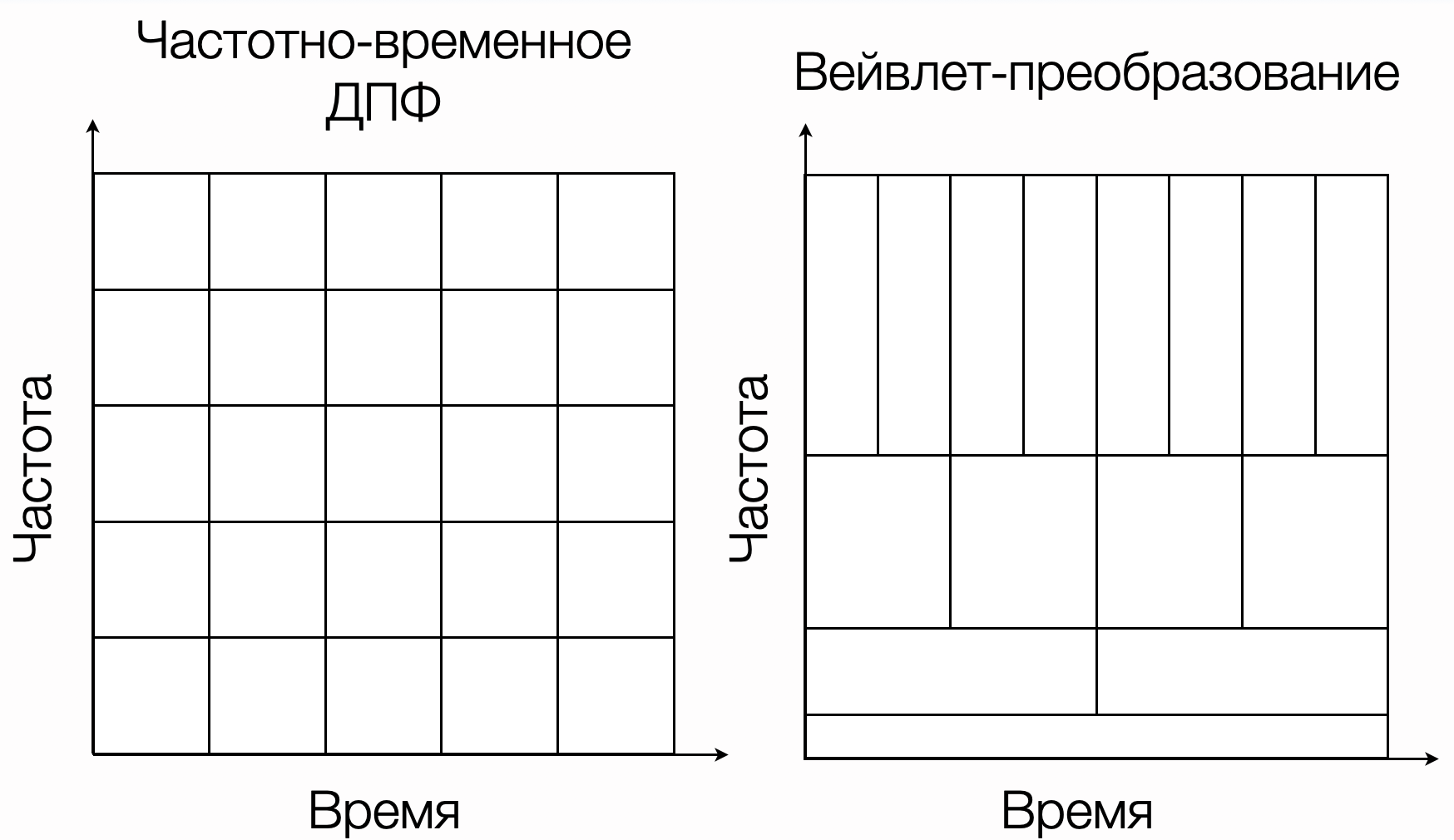
На нём показано разбиение частотно-временной плоскости на анализируемые участки, имеющие одинаковую площадь. В случае с ДПФ, все участки одинаковы по форме, что приводит к вышеупомянутой неопределённости. В случае с вейвлет-преобразованием, на низких частотах анализируются длинные отрезки времени (получаем хорошее разрешение по частоте), а на высоких частотах анализируются короткие отрезки времени (в результате чего получаем хорошее разрешение по времени).
Не нужно лишних слов, перейдём к примеру. Как мы делали на лекции по частотно-временному преобразованию Фурье, создадим сигнал, состоящий из трёх друг за другом идущих синусоид с частотами 10 Гц, 20 Гц и 30 Гц, построим график ДПФ данного сигнала, а затем воспользуемся функцией cwt Matlab, чтобы произвести вейвлет-преобразование. В качестве вейвлета выберем вейвлет Морле.
clear, clc, close all
fs = 100;
f1 = 10;
f2 = 20;
f3 = 30;
% Задаём сигнал с тремя подряд идущими частотами
t1= 0 : 1/fs : 1-1/fs;
lt1 = length(t1);
x(1 : lt1)=sin(2*pi*10*t1);
t2= 1 : 1/fs : 2-1/fs;
lt2 = length(t2);
x(lt1 + 1 : lt1 + lt2) = sin(2*pi*20*t2);
t3= 2 : 1/fs : 3-1/fs;
lt3 = length(t3);
x(lt1 + lt2 + 1 : lt1 + lt2 + lt3) = sin(2*pi*30*t3);
t = [t1 t2 t3];
N = length(t);
subplot(2,1,1)
plot(t,x), grid on, title('Сигнал с тремя подряд идущими частотами')
xlabel('Время'), ylabel('Амплитуда')
X = 2*abs(fft(x))/N;
f = 0: fs/N : fs-fs/N;
subplot(2,1,2)
stem(f,X), grid on, title('Спектр данного сигнала')
xlabel('Частота'), ylabel('Амплитуда')
figure
cwt(x,'amor',fs)
Запустим скрипт и посмотрим на результаты. Нестационарный сигнал x и его ДПФ показаны ниже:
Вейвлет-преобразование от сигнала x:
Серым цветом на графике показана зона недостоверности, которая связана с краевым эффектом вейвлет-преобразования. На графике отчётливо видны три частотные составляющие с частотами, которые были заданы в скрипте (можете проверить с помощью курсоров — следует учесть, что шкала частоты нелинейная).
В Matlab имеется возможность управлять набором фильтров (вейвлетов), которые будут использоваться функцией cwt. Например, мы знаем, что наш сигнал находится в диапазоне от 10 до 30 Гц и хотим проанализировать его с набором вейвлетов, соответствующих этому диапазону частот. Для этого можно дополнить предыдущий листинг следующим образом:
% формируем набор фильтров
fb = cwtfilterbank('SignalLength',numel(x),'SamplingFrequency',fs,...
'FrequencyLimits',[10 30]);
figure
freqz(fb)
% применяем сформированный набор фильтров
figure
cwt(x,'FilterBank',fb)
В результате получим набор АЧХ сформированных фильтров:
и вейвлет-преобразование с применением этих фильтров:
С помощью вейвлет-анализа также можно определить разрывы функции. Давайте создадим синусоидальный сигнал частотой 5 Гц и частотой дискретизации 100 Гц и попробуем убрать из него всего один отсчёт.
clear, clc, close all
fs = 100;
ts = 0: 1/fs : 3-1/fs;
x = sin(2*pi*5*ts);
% убираем из сигнала отсчёт с индексом 100
x(100) = [];
subplot(2,1,1)
plot(ts(1:length(ts)-1),x), grid on, title('Синусоида с разрывом')
xlabel('Время'), ylabel('Амплитуда')
% чтобы построить результаты функции cwt внутри subplot,
% приходится немного потанцевать с бубном
subplot(2,1,2)
[cfs,frq] = cwt(x,'amor',fs);
tms = (0:numel(x)-1)/fs;
surface(tms,frq,abs(cfs))
axis tight
shading flat
title('Вейвлет-преобразование')
xlabel('Время'), ylabel('Частота')
Давайте посмотрим на результат:
И что мы видим? Мы убрали всего один отсчёт из синусоидального сигнала, и это никак не заметно на графике во временной области. Я думаю, вы понимаете, что преобразование Фурье в этом случае тоже ничего не покажет (можете проверить, построив ДПФ от сигнала x). Зато на графике вейвлет-преобразования в районе отсчёта с индексом 100 (момент времени 1 с) явно виден всплеск.
Мы рассмотрели самые базовые понятия о вейвлет-преобразовании. На самом деле, его область применения очень широка: спектральный анализ, анализ данных, сжатие данных, удаление шумов, обработка изображений и многое другое, но об этом в другой раз.
Скачать конспект в pdf: Wavelet Transform Lecture – V.V. Leonidov.pdf
Comments (0)