Корреляция
Главными задачами корреляционного анализа являются выявление зависимости или сходства между какими-либо сигналами. Корреляционный анализ имеет широкое применение в различных областях: например, поиск изображения по образцу, поиск полезных сигналов “под шумами”, обработка сигналов радаров и т.п.
Корреляция в простом виде — это поэлементное произведение двух сигналов. Если получим большое число — сигналы похожи, если маленькое — нет:
(1) ![Rendered by QuickLaTeX.com \begin{equation*} r_{12} = \sum\limits_{n=0}^{N-1} x_1[n] \cdot x_2[n] \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-ccec7249dd68df880a59f55c2e937331_l3.png)
Однако, результат выражения (1) будет зависеть от количества отсчётов сигналов. Чтобы это учесть, результат нормируют на количество отсчётов ![]() :
:
(2) ![Rendered by QuickLaTeX.com \begin{equation*} r_{12} = \frac{1}{N}\sum\limits_{n=0}^{N-1} x_1[n] \cdot x_2[n] \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-66c64ca0b2e8aeb4eebe296e227a8006_l3.png)
Рассмотрим пример. Возьмём два меандра, сдвинутых по фазе на ![]() и посчитаем их корреляцию по формуле (2):
и посчитаем их корреляцию по формуле (2):
clear;
fs = 100;
ts = 0:1/fs:5-1/fs;
x1 = (square(2*pi*ts)+1)/2;
x2 = (square(2*pi*ts+pi)+1)/2;
subplot(2,1,1);
plot(x1), grid on;
xlabel('Временные отсчёты, n'), ylabel('x1[n]');
subplot(2,1,2);
plot(x2), grid on;
xlabel('Временные отсчёты, n'), ylabel('x2[n]');
r12 = sum(x1.*x2)
В результате выполнения скрипта получим графики сигналов x1 и x2 и значение корреляции r12 = 0.
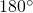
Получается, что сигналы похожи, а корреляция равна нулю. Значит, выражение (2) необходимо модифицировать и добавить временной сдвиг ![]() одного сигнала относительно другого:
одного сигнала относительно другого:
(3) ![Rendered by QuickLaTeX.com \begin{equation*} r_{12}[j] = \frac{1}{N}\sum\limits_{n=0}^{N-1} x_1[n] \cdot x_2[n+j] \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-1a71bf0eebe863d755bdd769adc01da4_l3.png)
Дополним предыдущий листинг и построим график корреляционной функции ![]() . Для этого воспользуемся функцией Matlab взаимной корреляции двух сигналов
. Для этого воспользуемся функцией Matlab взаимной корреляции двух сигналов xcorr:
figure;
[r12,lags] = xcorr(x1,x2);
plot(lags,r12), grid on;
xlabel('Временной сдвиг, j'), ylabel('r_{12}[j]');
Результат выполнения модифицированного кода показан ниже:
Из графика видно, что при нулевом сдвиге ![]() корреляция двух сигналов равна нулю
корреляция двух сигналов равна нулю ![]() , при дальнейшем сдвиге влево или вправо значение
, при дальнейшем сдвиге влево или вправо значение ![]() увеличивается, затем снова уменьшается. Это происходит периодически, однако амплитуда пиков
увеличивается, затем снова уменьшается. Это происходит периодически, однако амплитуда пиков ![]() постепенно уменьшается к краям графика. Наверняка многие ожидали увидеть в качестве
постепенно уменьшается к краям графика. Наверняка многие ожидали увидеть в качестве ![]() периодический треугольный сигнал. Однако, из-за того, что сигналы
периодический треугольный сигнал. Однако, из-за того, что сигналы x1[n] и x2[n] имеют конечную длину, получается, что при сдвиге одного сигнала относительно другого, наступает момент, когда они не перекрываются и вместо парных произведений отсчётов получаем произведения на “пустые отсчёты”, или на ноль. Чем дальше два сигнала сдвигаются друг относительно друга, тем больше получается произведений с нулевым результатом, тем меньше получается результирующая ![]() . Эта неприятность называется краевой эффект.
. Эта неприятность называется краевой эффект.
Один из способов убрать влияние краевого эффекта — увеличить длину одного из сигналов (например, x2[n]) в два раза:
figure;
N = length(x1);
x2 = [x2 x2]; % добавляем в конец x2 его копию
r12=zeros(1,N);
% расчёт корреляционной функции:
for j=1:N-1
r12(j) = sum(x1.*x2(j:j+N-1));
end
plot(r12), grid on;
xlabel('Временной сдвиг, j'), ylabel('r_{12}[j]');
В результате получим график:
Так гораздо лучше. А что, если амплитуду сигнала x2[n] увеличить в два раза? Отредактируем строку 7 листинга “Корреляция двух меандров, часть 1”:
x2 = (2*square(2*pi*ts+pi)+2)/2;
Запустим заново скрипт и увидим, что амплитуда треугольного сигнала возросла вдвое:
Так как же оценить степень схожести сигналов? Какое значение ![]() есть хорошо, а какое — плохо? Чтобы вы не задавали таких вопросов, придумали нормированную корреляционную функцию, в которой результат может принимать значения только в диапазоне
есть хорошо, а какое — плохо? Чтобы вы не задавали таких вопросов, придумали нормированную корреляционную функцию, в которой результат может принимать значения только в диапазоне ![]() . Значению 1 соответствует полная корреляция (сигналы абсолютно похожи или зависимы), нулю соответствует полное отсутствие корреляции (сигналы абсолютно непохожи или независимы) и -1 соответствует полная противоположная корреляция (сигналы находятся в противофазе). Нормированная корреляционная функция имеет вид:
. Значению 1 соответствует полная корреляция (сигналы абсолютно похожи или зависимы), нулю соответствует полное отсутствие корреляции (сигналы абсолютно непохожи или независимы) и -1 соответствует полная противоположная корреляция (сигналы находятся в противофазе). Нормированная корреляционная функция имеет вид:
(4) ![Rendered by QuickLaTeX.com \begin{equation*} \rho_{12}[j] = \frac{r_{12}[j]}{\frac{1}{N} \sqrt{\sum\limits_{n=0}^{N-1} x_1^2[n] \cdot \sum\limits_{n=0}^{N-1} x_2^2[n]}} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-b0b358b95958fd77c3d339d8d159a83d_l3.png)
По аналогичной формуле корреляцию будет считать Matlab, если к функции xcorr добавить ещё один параметр 'normalized' или 'coeff'.
Автокорреляция
А что, если в выражении (3) в качестве сигнала ![]() также взять сигнал
также взять сигнал ![]() и начать сравнивать его с самим собой? Получится автокорреляционная функция:
и начать сравнивать его с самим собой? Получится автокорреляционная функция:
(5) ![Rendered by QuickLaTeX.com \begin{equation*} r_{11}[j] = \frac{1}{N}\sum\limits_{n=0}^{N-1} x_1[n] \cdot x_1[n+j] \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-57226796ffd7de544a4f55dc54974740_l3.png)
Некоторые зададут вопрос: “Что за бред? Зачем это нужно?”. Во-первых, для определения, является ли исследуемый сигнал случайным, или же в нём есть периодическая составляющая. Если есть периодическая составляющая, можно более явно увидеть, какая у неё частота.
Рассмотрим пример. Создадим зашумлённый синусоидальный сигнал частотой 0.5 Гц и построим его график. Затем построим график автокорреляционной функции этого сигнала и взглянем на него.
clear;
Fs = 10;
ts = 0: 1/Fs : 10-1/Fs;
N = length(ts);
x = 0.1*sin(2*pi*0.5*ts);
x = awgn(x,20);
subplot(2,1,1)
plot(x), grid on, title('Исходный сигнал')
xlabel('Время')
[xc, lags] = xcorr(x,'unbiased');
subplot(2,1,2)
plot(lags/Fs,xc), grid on, title('Автокорреляционная функция')
xlabel('Временной сдвиг')
Результаты выполнения скрипта показаны ниже.
Из верхнего графика сложно сделать вывод о периодичности сигнала, однако, если взглянуть на график его автокорреляционной функции (снизу), то все сомнения отпадают.
А как же будет выглядеть автокорреляционная функция (АКФ) для случайного сигнала? Рассмотрим на примере. Разработаем скрипт, генерирующий случайный сигнал амплитудой от -1 до 1, состоящий из 256 отсчётов. Затем построим график самого сигнала и его АКФ:
clear;
% параметры случайного сигнала
N = 256;
a = -1;
b = 1;
% случайный сигнал
x = (a + (b - a) * rand(1, N));
% его АКФ
[c,lags] = xcorr(x,'coeff');
subplot(2,1,1);
plot(x), grid on, title('Случайный сигнал')
xlabel('Временные отсчёты, n'), ylabel('x[n]');
subplot(2,1,2);
plot(lags,c), grid on, title('АКФ случайного сигнала')
xlabel('Временной сдвиг, j'), ylabel('c[j]');
Результат выполнения скрипта представлен ниже:
Из рисунка видно, что для случайных сигналов график автокорреляционной функции имеет свой максимум при ![]() и стремится к нулю с увеличением сдвига
и стремится к нулю с увеличением сдвига ![]() .
.
Также, стоит обратить внимание, что при ![]() выражение (5) принимает вид:
выражение (5) принимает вид:
(6) ![Rendered by QuickLaTeX.com \begin{equation*} r_{11}[0] = \frac{1}{N}\sum\limits_{n=0}^{N-1} x_1^2[n] = S \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-77a4549ceab5869d0003f06367469f99_l3.png)
где ![]() — нормированная энергия сигнала.
— нормированная энергия сигнала.
Корреляция изображений
Помимо одномерных сигналов, корреляционный анализ можно проводить и с двумерными сигналами. Например, с изображениями для поиска какого-либо шаблона в другом изображении. Корреляционная функция для изображений может иметь вид:
(7) ![Rendered by QuickLaTeX.com \begin{equation*} \gamma(u,v) = \frac{\sum\limits_x\sum\limits_y(f[x,y]-\overline{f}_{u,v})(t[x-u,y-v]-\overline{t})}{\sqrt{\sum\limits_x\sum\limits_y(f[x,y]-\overline{f}_{u,v})^2 \sum\limits_x\sum\limits_y(t[x-u,y-v]-\overline{t})^2}} \end{equation*}](https://leonidov.su/wp-content/ql-cache/quicklatex.com-c94ebb9a0c1fb122b87948537817a501_l3.png)
где:
![Rendered by QuickLaTeX.com f[x,y]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-797cb940db17f34eda8f63d786d25b86_l3.png) – исходное изображение
– исходное изображение![Rendered by QuickLaTeX.com t[u,v]](https://leonidov.su/wp-content/ql-cache/quicklatex.com-28103dc5224879c046c5487170e18a6f_l3.png) – искомый шаблон
– искомый шаблон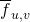 – среднее значение интенсивности изображения под шаблоном
– среднее значение интенсивности изображения под шаблоном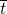 – среднее значение интенсивности шаблона
– среднее значение интенсивности шаблона
Именно такой формулой пользуется Matlab при расчёте взаимной корреляции двумерных сигналов с помощью функции normxcorr2.
Скачать конспект в pdf: Correlation Lecture – V.V. Leonidov.pdf
Comments (0)